Digitaalisen oskilloskoopin alias ilmiöt. Osa 1.

Teoriaa ja käytäntöä alias ilmiöstä joka on usein esillä puhuttaessa digitaalisista oskilloskoopeista. 

Tässä ei käsitellä näyttökuvan aliasointia liittyen kuvan pixeleihin. Se on kokonaan toinen asia.
Toki sitäkin voi esiintya ja esiintyy silloin tällöin myös digitaaliskoopissa kun pixelijako ja kuvan yksityiskohdat osuu sopivasti.

Alias ilmiö, aliasointi, on hyvä ymmärtää jotta välttyy vääriltä tulkinnoilta tai että osaa minimoida sen vaikutuksia. Samplenopeus, näytenopeus, suhteessa tutkittavaan signaaliin on tässä asiassa erittäin merkittävässä roolissa.

Aliasointiin ja samplenopeuteen liittyvät seikat ovat tärkeitä huomioitavia oskilloskooppia valittaessa erilaisiin käyttötarkoituksiin ja erilaisille signaalityypeille.

Tämä liittyy hyvin läheisesti myös toiseen esitykseen jossa enemmän asiaa Sin(x)/x ym interpoloinnin vinkkelistä katsottuna.
Se kannattaa lukea yhdessä tämän kanssa.  

Joissain kohdin pistän hiukan mutkia suoraksi, kuitenkin niin että valtavia vääristymiä ei synny, muuten pitäisi kirjoittaa kirja. (Olen siis kohtalaisesti pyrkinyt siihen ettei ajauduta kovin kauaksi todellisuudesta eikä suureen ristiriitaan teorioiden kanssa vaikka mutkia oiotaankin)

Digitaalisten oskilloskooppien yhteydessä puhutaan usein alias ilmiöstä. Joskus sitä sekoitetaan myös siihen mikä liittyy kuvan muodostamiseen TFT tms "pixeli"monitorille sen resoluutiolla. Televisioissa kaikkien tuntema "Moire" ilmiö on sekin jonkun asteinen sukulainen tälle. En käsittele sitä enkä sen kaltaisia kuvanmuodostukseen liittyviä kosmeettisia asioita. Joissakin oskilloskoopeissa on ns "anti-alias" asetus joka joskus voi tarkoittaa myös tuota kosmeettista kuva-aliasoinnin vähentämistä.

Se mitä varsinaisesti tarkoitetaan digitaalisista oskilloskoopeista puhuttaessa signaalin alias ilmiöllä liittyy laitteen samplenopeuteen (näytteen oton taajuus tai näytteiden aikaväli - intervalli) sekä signaalin ominaisuuksiin joista nuo näytteet otetaan.

Yksinkertasesti: Oletetaan että AD muunnin ottaa tasavälein näytteitä jatkuvasti jollakin näytetaajuudella. Kaikki signaalin taajuuskomponentit jotka pääsevät tasavälein näytteittävään AD muuntimeen ja ovat taajuudeltaan suurempia kuin puolet näytetaajuudesta muodostavat aliaksen. (Kuva 1.)
Ei ole mitään keinoa estää sitä tai vähentää sitä. Jos joku sellaisesta puhuu hänellä on käytössään joku ns "vaihtoehtoinen totuus" tai sitten puhe ymmärretään väärin. Käytännössä ongelmat alkavat jo jonkun verran alempana kuin näytetaajuus/2.

Kaikki seuraava koskee nimenomaaan ja vain ns "real time" oskilloskooppia. Sellainen ottaa käytössä olevalla samplenopeudella yhdellä vaakapyyhkäisylla kaikki näytteet. Puhutaaan myös ns "single" shot samplenopeudesta. (on muitakin tapoja kuten esim ns "Equal Time" tyyli (monia erilaisia) joissa yhdellä pyyhkäisyllä otetaan näytteet, sitten seuraaavalla  kierroksella lisää ja tätä jatketaan kunnes näytteitä onn saatu riittävästi. Tämä tapa ei svellu nopeasti muuttuville signaaleille enkä  puhu niistä sen enempää. Mikäli oskilloskooppi on sellainen tämä juttu ei sovellu niihin, lukuunottamattaa tilannetta jossa sellaista oskilloskooppia käyetään sillä samplenopeudella joka on kyseisen oskilloskoopin ns "single shot" näytenopeus.

Alkuun yksinkertainen piirros siitä mistä alias ilmiössä on kyse.

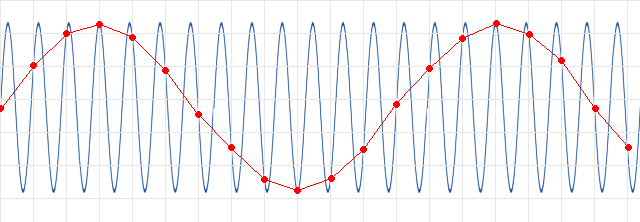
Kuva 1.
Kun tulevan signaalin (kuvassa sininen) taajuus on suuri verrattuna näytetaajuuteen (punaiset näytepisteet) ei alkuperäistä signaalia voida rekonstruoida näytepisteiden pohjalta. Kuvittele että punaisten pisteiden kautta vedettäisiin viivat. Alkuperäisen, kuvassa esitetyn siniallon, sijaan näytettäisiin tuo "alias" siniaalto mutta sen taajuus olisi aivan väärä. Katso jäljempänä olevia osskilloskoopin ruutukuvia.





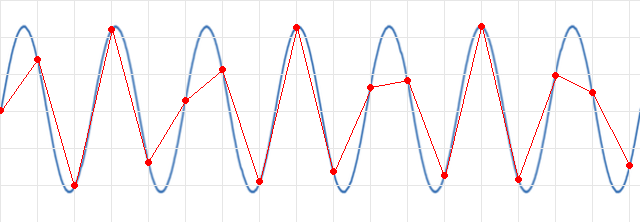
Jos meillä olisi noin 2.5 kertainen näytetaajuus (punaiset näytepisteet) signaalin taajuuteen nähden ja niiden kautta vedettäisiin viivat olisi meillä jo jonkunlainen käsitys signaalista, ainakin sen taajuudesta.  Mikäli punaisten suorien viivojen sijasta käytössä olisi Sin(x)/x interpolointi olisi tulos jonkinlainen siniaalto jossa kuitenkin olisi paljon tasovaihtelua jaksolta toiselle. Nopeuden vuoksi Sin(x)/x interpolointi tapahtuu hyvin lyhyeltä aikaväliltä. Mikäli voisi käyttää pitkää näytejonoa ja signaali siis olisi myös ns jatkuva, tulos olisi luonnollisesti parhaimmillaan erittäin lähellä alkuperäistä. Näin ei kuitenkaan oskilloskoopeissa tehdä yleensä jotta se toimii myös nopeissa signaaalin muutoksissa, kuten vaikkaapa kertapulssien nousevilla reunoilla. Katso jäljempänä olevia oskilloskoopin ruutukuvia.





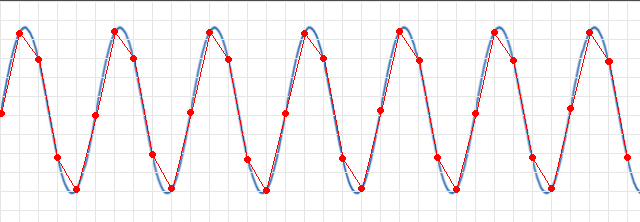
Jos meillä olisi noin 5 kertainen näytetaajuus (punaiset näytepisteet) signaalin taajuuteen nähden ja niiden kautta vedettäisiin viivat olisi meillä jo jonkunlainen käsitys signaalista, ainakin sen taajuudesta. Mikäli punaisten suorien viivojen sijasta käytössä olisi Sin(x)/x interpolointi olisi tulos erittäin lähellä alkuperäistä signaalia. Sin(x)/x interpoloinnin jälkeen tasojitteriä näkyisi tuskin näytöllä erottuvaa määrää. Katso jäljempänä olevia oskilloskoopin ruutukuvia.



Nyquist-Shannon teoreeman mukaan näytetaajuuden tulee olla vähintään kaksinkertainen signaalin taajuuteen nähden. Jotta silloin voitaisiin rekonstruoida signaali pitää täyttää monta tiukkaa ehtoa. Niitä ei kaikkia täytetä missään tiedossani olevassa oskilloskoopissa.

Ohittamalla monta yksityiskohtaa voidaan käytännöstä sanoa että näytetaajuuden tulee olla selvästi suurempi kuin signaalin taajuus kerrottuna kahdella. Jonkinasteinen  nyrkkisääntö  voisi olla että näytetaajuuden tulee olla vähintään 2,5 kertaa signaalin taajuus kun tutkittava signaali on siniaalto  ja se rekonstruoidaan näytepisteistä Sin(x)/x interpoloinnilla. Useinmiten tämä tuottaa vielä varsin ikävän näköisen  kuvan siniaallosta jossa esiintyy runsaasti muuun muassa tasovaihtelua. Kuitenkin monien lähteiden (Esim. Tektronix, Keysight)  mukaan sitä pidetään vähimmäisvaatimuksena.

Asia on suhteellisen yksinkertainen kun katsoo ylläolevia kuvia. Kuva on kuitenkin aivan erikoistapaus. Pitää muistaa että oskilloskoopin on tarkoitus kuvata se signaali joka on meille tuntematon. Emme tarvitse oskilloskooppia lainkaan mikäli meillä on tarkka tieto signaalista. Oskilloskooppia tarvitaan kun halutaan tietää minkälainen meitä kiinnostava signaali on tai onko se sellainen kuin sen pitäisi olle.

Oskilloskoopilla siis tutkitaan enemmän tai vähemmän "tuntematonta" josta oskilloskoopilla halutaan saada riittävän tarkka käsitys. 

Kun puhutaan alias ilmiöstä tärkeää on näytteenottotaajuus ja signaalin sisältämät taajuuskomponentit.

Kauniita kanttiaaltoja ja hienoja saha- ja muita aaltomuotoja esiintyy koulukirjoissa. Ikäänkuin ideaaleja signaaleja joita ei esiinny  reaalimaailmassa. Usko vaan, niitä ei ole, niitä ei tule, eikä niitä ole koskaan ollut missään - paitsi siinä kirjan kuvassa ja mielikuvituksessa. Niitä teoreettisia kuvia kuitenkin tavitaan. 

Usein kuulee kysyttävän siitä miksi kanttiaalto ei näytä lainkaan kanttiaallolta. Pitää muistaa että aaltomuodot jotka ovat muuta kuin puhdasta jatkuvaa siniaaltoa koostuvat joukosta eri taajuuksisia ja tasoisia siniaaltoja. Jotta oskilloskooppi kykenisi piirtämään signaalin oikein, sen tulisi kyetä näkemään kaikki signaalin taajuuskomponentit mahdollisimman tarkoin jotta niiden summa vastaa signaalia.

Kanttiaallon tapainen on kohtalaisen hyvä esimerkki. Niitä esiintyy usein signaaleina joita oskilloskoopilla tutkimme, samoin kuin tapauksia joissa signaalin tasossa tapahtuu jokin muu äkillinen muutos.  Yleensä haluamme tutkia jotain jossa tapahtuu muutoksia. Aina kun jotain muuttuu astuu kuvaan mukaan muutoksen suuruus ja kuinka muutos tapahtuu ajan suhteen.

Otetaan siis suorakaideaalto esimerkiksi.
Ajatellaan että meillä on 1MHz kanttiaalto jossa nousu- ja laskunopeus on hyvin nopea. Sen perustaajuus eli 1. harmoninen on  1MHz.
Kanttiaalto (Puhdas) koostuu perustaajuuden lisäksi parittomista harmonisista siniaalloista. 1MHz on tässä 1. harmoninen eli perustaajuus. 2MHz jää väliin. 3. Harmoninen esiintyy, 4. jää pois. 5. esiintyy, 6. jää pois, 7. esiintyy jne. Ideaalitapauksessa  parittomia harmonisia aina lähes äärettömyyteen saakka. Samalla kuitenkin kun harmonisen järjestysnumero kasvaa sen harmonisen taso on alempi. 3.harmonisen taso 1/3 ja 5. harmonisen taso 1/5 osa jne. 

Mitä enemmän  tutkittavassa kantissa olevia harmonisia oskilloskooppi kykenee oikein havaitsemaan sitä lähempänä kuva on sitä todellista tutkittavaa kanttiaaltoa. Luonnollisesti enempää ei tarvitse nähdä kuin ne mitä tutkittaavassa on. Nyt siis kyseessä oli jyrkkäreunainen.  Mikäli saamme kohtalaisen oikein 7. 9. tai jopa 11. harmonisen näyttää kanttiaalto melko hyvältä mutta ei suinkaan vielä täydelliseltä.  Vähimmäisvaatimuksena voisi sanoa että 5. harmoninen tulisi ainakin olla mukana mainittavasti vaimentumattomana, silloin se jo muistuttaa "kanttiaaltoa". 

Tilanne on kuitenkin usein paljon vaativampi. Meille saattaakin olla olennaista myös kyetä mittaamaan niiden muutosreunojen nopeus. Jos signaalin nousunopeus on hyvin nopea ja skoopin ruudulla haluamme nähdä 3,5ns nousunopeuden meillä tulee olla vähintään 100MHz  oskilloskooppi.

Oskilloskoopin nimellinen "taajuus"  tarkoittaa periaatteessa sitä taajuutta jolla signaalin taso on pudonnut 3dB sovittuun matalataajuiseen referenssitasoon nähden.
Puhutaan ns Gauss tyyppisestä taajuusvasteen muodosta.

Puuttumatta yksityiskohtiin voidaan nyrkkisääntömäisesti sanoa että oskilloskoopin nousunopeus nanosekunteina on 350/nimellistaajuus MHz. (nousunopeus mitattuna signaalin 10 ja 90% väliltä.) 100MHz oskilloskoopin nousunopeus on siis 3,5ns. Usein -3dB piste on jonkin verran ylempänä kuin oskilloskoopin mainittu taajuusraja.  Huomaa että joissain oskilloskoopeissa taajuusvasteen muoto on toisenlainen ja silloin nousunopeus ei ole tuon nyrkkisäännön mukainen.
Tuo siis on silloin oskilloskoopin itsensä nousunopeus.
Jos oskilloskoopin nousuaika on 3.5ns ja signaalin nousuaika on 3.5ns emme suinkaan näe 3.5ns nousunopeutta ruudulla. Näemme noin 5ns nousunopeuden. Virhettä on yli 40%.   Signaalin ja oskilloskoopin yhdistetty nousunopeus voidaan laskea:  SQR((rtSign^2)+(rtOsc^2)).
Jos signaalin nousunopeus olisi 3.5ns ja haluaisimme mitata sen ilman että oskilloskoopin nousunopeuden aiheuttaama virhe on yli 3% tarvisimme oskilloskoopin jonka nousunopeus on alle 0.9ns eli noin 400MHz oskilloskoopin!  Tähänkin liittyvää enemmän oskilloskoopin valintaa koskevassa kertomuksessa.

Edellämainittu liittyy helposti ja usein puheena olevaan alias ilmiöön.

Tarkastellaan hiukan miksi. Seuraavassa kuvassa esimerkki taaajuusvasteen muodosta. Kyseessä Siglent SDS1102X. (huomaa että kyseessä ei ole skoopin taajusvasteen testaus - määrittely. Kuvaa ei pidä katsoa niin että ahaa, tuollainen on taajuusvate jos hankin ko. skoopin. Kuva soveltuu käytettäväksi vain tämän jutun tekstiin liittyvänä kuvituskuvana.

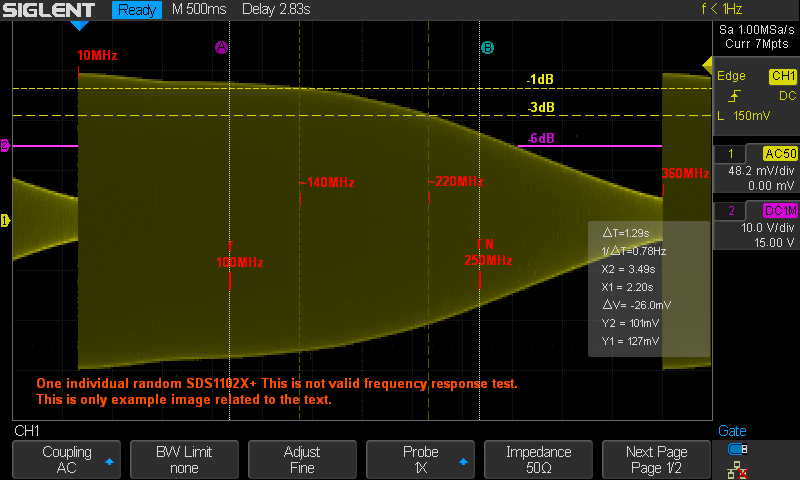
Kuvassa on pyyhkästy taajuusalue  10MHz - 360MHz.  Kuvaaan on merkitty skoopin 100MHz nimellisstaajuus. joka on merkattu käyttäen Gate kursoria A,  sekä mittauskursoreilla  -1dB (140MHz) sekä -3dB (220MHz). 
Sitten tulee tärkeä taajuus:  fN  on Nyquist rajataajuus. (näytetaajuus/2).   Tässä se on 250MHz. (2 kanavaa käytössä max 500MSa/s . Mikäli 1 kanava käytössä, max 1GSa/s)

Alias ilmiön kannalta tuo Nyquist taajuus ( fN ) on aivan olennainen asia. Se on sellainen ns ehdoton raja ja kaikki se mitä on fN yläpuolella näkyy alias ilmiöinä.
Monesti virheellisesti puhutaan että jos taajuus on alle Nyquist taajuuden sitten kaikki on ok. Ei, todellakaan niin ei ole. Siinä vaan on luetun ymmärrys jäänyt vähiin tai kuultu "kaverilta" tai joku "guru" sepittelee omiaan. En mene syvemmälle teoriaan ja käytäntöön mutta tuo vaan kaatuu siihen että yksikään käytännön oskilloskooppi ei täytä niitä jakaista ehtoa jotka pitäisi kaikki täyttyä jotta tuo olisi tosi. Eli, lukekaa vaan uudelleen sekä Nyquist että esimerkiksi Chris Rehorn (Hwlett-Packard).  Käytännössä raja osuu vastaan jossain noin fN/1.25 paikkeilla. (noin sampletaajuus/2.5).   Mutta, esimerkiksi varsinaiset alias taajuudet lasketaan luonnollisesti tarkalleen Nyquist taajuuden tai sampletaajuuden pohjalta.
 
Mitä se alias taajuus on? 
Esim jos Nyquist taajuus on 250MHz niin jos signaali olisi 350MHz syntyisi 150MHz alias taajuus jonka saattaisimme nähdä skoopin ruudulla, sen 350MHz sijasta. Vastaavasti 260MHz näkyisi 240MHz taajuutena. Tämän osalta on muistettava nyt sitten se että esimerkiksi kanttiaallon harmoniset ovat ihan samoin signaalitaajuuksia vaikka ne eivät erikseen siniaaltoina näy mutta ne aiheuttaavat alias ilmiötä (se ilmiö näkyy esim  kantin nurkkien "jitterinä" tai "wobblerina" miten sitä nimittelevätkin. On hyvä muistaa että ne kanttiaallonkin harmoniset noudattaa samaa perieetetta joilla ne muuntuvat toisiksi (alias) taajuuksiksi!

Kun katsot taajuusvastetta kuvassa huomaat että Nyquist taajuuden yläpuolella edelleenkin skoopin sisääntulosta tulee AD muuntimelle signaalia ja kuvassa jopa niin että jännitetaso on vaimentunut vain noin puoleen. Tämä tietenkin  vain kun samplenopeus on 500MSa/s.  Jos samplenopeus olisi samalla taajuusvasteella 1GSa/s olisi Nyquist taajuus (500MHz) niin kaukana että sellaset taajuudet vaimenevat jo erittäin paljon ja vaaraa alias ilmiölle ei paljoa ole. (SDS1102X kun yksi kanava käytössä)

Jos epäilet että signaalissa on riittävän voimakkaita taajuuskomponentteja jotka menevät yli kulloisenkin Nyquist rajan tai hyvin lähelle sitä ja epäilet signaalia katsoessasi alias ilmiöiden mukana oloa. Kytke tilapäisesti toinen kanava pois, samplenopeus nousee. Jos olet hitailla t/div nopeuksilla jaa samplenopeus alhainen ja siis Nyquist raja alhainen myös, kokeile nostaa samplenopeutta tilapäisesti ja totea häviääkö ilmiö. Maksimoi samplenopeus mahdollisuuksien mukaan. Jos keinot loppuvat, ja signaalissa korkeita taajuuskomponentteja jotka aiheuttavat aliasiointia kokeile ylempien taaakjuuksien suodaattamista pois. Jos taas ne ylemmät taajuudet ovat sinulle tärkeitä. Silloin sinulla on liian hidas oskilloskooppi.


Seuraavassa hiukan demonstraatioita kuvin.
Osassa esimerkkikuvia joissa olen käyttänyt tarkoituksellisesti alhaisia signaalin taajuuksia sekä alhaisia samplenopeuksia jolloin on ollut helpompi tehdä nuo esimerkit. Samoin jää pois oskilloskoopin analogisen etuosan kaistaleveyden merkittävät vaikutukset sekä voin hallita paremmin sisääntulevan signaalin ominaisuuksia. Tässä siis signaali on tunnettu ja katsotaan oskilloskooppia ikäänkuin se skooppi olisi tutkittava laite. Yleensä oskilloskooppia käytetään toisin  päin eli sillä analysoidaan enemmän tai vähemmän tuntematonta signaalia.  Siinä on usein avuksi mikäli tuntee oskilloskoopin käyttäytymistä.

On helppo saada signaali jonka nousevan reunan nousuaika on säädettävissä 1000ns - 5000ns mutta minulla ei ole signaalilähdettä jolla voisin tuottaa helposti 1,0 - 5,0 ns nousuaikaisen signaalin siten että voin säätää nousuaikaa suhteellisen tarkasti. Siksi valitsin samplenopeudeksi 1MSa/s. Se on suoraan 1:1000 jos ajatellaan 1GSa/s ja siinä suhteessa myös nousuaika 1000ns vastaa 1ns. Mikä tässä jää pois on analoginen taajuusvaste ennen AD muunninta sekä ongelmat signaalin siirrossa oskilloskoopille. Näin saa  asiasta selkeämmän jolloin voi keskittyä vain tuohon digitoinnin ja siitä kuvanmuodostuksen alias ilmiöihin.


Aluksi kolme kuvaa joissa kaikissa signaali sama ja raskaasti liian alhainen samplenopeus.
Signaalin taajuus 900kHz. Samplenopeus 1MSa/s. Tästä puolet, eli Nyquist raja, on 500kHz.
Tämä on esimerkki klassisesta perus alias ilmiöstä joka on usein esimerkkinä.
Useimpia esimerkkikuvia kannattaa katsoa siten että kuvan zoomattu alaosa olisi se jota katsellaan. Zoomaus on tehty juuri siksi että voin käyttää hidasta vaakanopeutta jotta olen saanut samplenopeuden putoamaan  tässä tapauksessa 1MSa/s kun olen lisäksi ottanut 2 kanavaa käyttöön sekä rajoittanut muistin minimiin.
Näillä alhaisilla taajuuksilla on helpompi demonstroida. Sama tapahtuu jos kerrot tai jaat samplenopeuden ja käyteyn taajuuden samalla jollain luvulla. Edellyttäen tietenkin että oskilloskoopin analogisen tulokanavan kaistaleveys riittäisi.

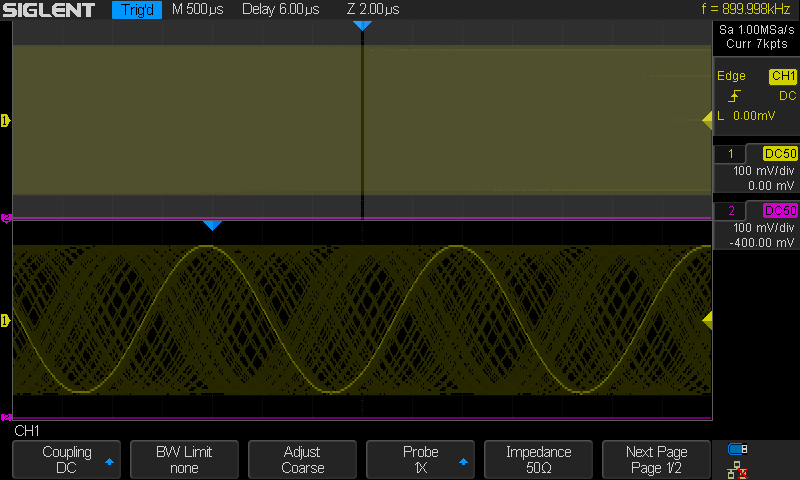
Kuvassa näkyy 100kHz siniaalto. Mitä ihmettä. Signaalinhan piti olla 900kHz.
Onko tutkittava signaali jostain syystä  alempi kuin luulin. huomio kiintyy myös siihen että kuva "vilisee" koko ajan enkä saa triggausta toimimaan. Ompas kurja oskilloskooppi. Vai onko.
Sampletaajuus 1MHz. Signaali 900kHz. Nyquist raja on 500kHz. Jos katsoisi tätä tilannetta FFT analysaattorilla. Sekin näyttäisi 100kHz signaalia. Voi mielessään ajatella että Nyquist raja on ikääkuin peili. Samoin 0 taajuus.  Kun Nyquist seinäpeiliin 500kHz kohdalla osuu 900kHz se ylimenevä osuus 400kHz ikäänkuin heijastuu siitä takaisin päin ja jatkaa matkaa kohti 0 peiliä mutta ei sentään pääse sinne saakka vaan 100kHz kohdalle. Jos taajuus olisi vielä suurempi, sanotaan vaikka 1200kHz. Hmm... 500kHz kohdalta takaisin päin nyt 700kHz. Mutta siitä 500kHz takaisin päin tulee 0 vastaan ja käänytään takaisin, jäljellä on vielä 200kHz. Saadaan siis taajuus 200kHz. Siinä näkyisi FFT analyysillä piikki ja ylläolevassa kuvassa näkyisi 200kHz siniaalto sen 1200kHz aliaksena.

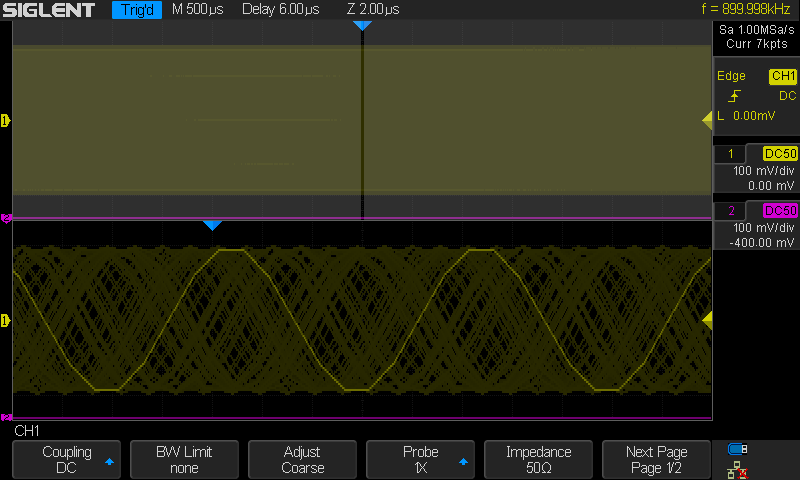
Sama kuin edellä mutta Sin(x)/x interpolaatio vaihdettu suoriksi viivoiksi. 

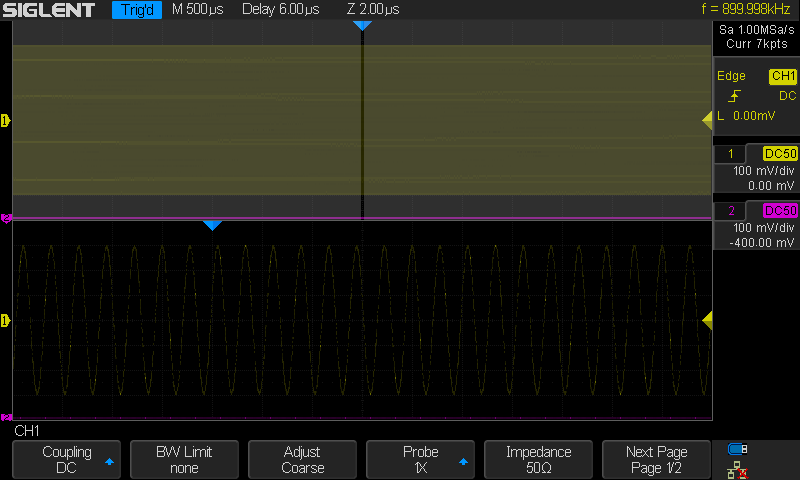
Nyt tapahtuu kummia.
Näytöksi valittu pelkät pisteet eikä niiden väliin piirretä mitään. Ei suoraa eikä Sinc interpolaatiota.  Kuinka kuvassa kuitenkin nyt näkyy 900kHz kaunis siniaalto. Kaiken lisäksi triggauskin toimii. Eihän se näin pitänyt mennä - vai.  No ei se menekään niin. Katso tarkasti. Näet hiukan kirkkaampia pisteitä, katsopa jos näkisit vain ne, miltä signaali silloin näyttäisi. Siinähän se on tuttu 100kHz. Vertaa edelliseen kuvaan ja sitä edelliseen. (sama signaali, eri näyttö- ja interpolointitapa).
 
Selitys.
Joka kerta kun skooppi tekee yhden vaakapyyhkäisyn se tuottaa yhden noiden kirkaampien pisteiden mukaisen näytejonon. Koska siinä ei ole mitään sykronointia näytekellon ja signaalin välillä, on joka pyyhkäisyllä pisteet eri kohdista signaalia. Signaali on ns jatkuva joten se pysyy muuttumattomana. Kerta toisensa jälkeen ruudulle tulostetaan nuo pisteet ja lopulta niitä on otettu niin monesta eri sijainnista että niiden pisteiden jäljet piirtävätkin alkuperäisen signaalin. Tässä tapauksessa kun on hidas pyyhkäisyaika olen käyttänyt persitence asetusta jolloin ns vanhat pyyhkäisyt jäävät hiukan himmeämpinä näytölle persistence asetuksen määräämäksi ajaksi. Kun persistence ajan (ns jälkiloisto) kello käy, vanhimmat pisteen katoavat ja uudemmat jää näytölle.
Useissa tilanteissa ei tarvita persistence ajastinta koska vaakapyyhkäisyjä toistetaan niin nopeasti että dataa näytölle ehtii kertyä paljon ennen kuin uusi kuvaruudullinen päivitetään. Sen sijaan mikäli kyseessä olisi nopeasti muuttuva signaali, tällä tavalla ei saataisi mitään järjellistä. (Tämä muistuttaa hivenen ns Equal Time sample moodia mutta ei ole kuitenkaan se. Tästä ei myöskään ole hyötyä silloin kun operoidaan lähellä oskilloskoopin nimellistaajuutta ja sen yli.)

Huomaa että tätä asetusta kannattaa opetella käyttämään hyödyksi erilaisissa tilanteissa. Joissain tilanteissa se myös auttaa sevittämään mahdollisen alias ilmiön. Ylläolevat eivät ole se ainoa tapa jolla alias ilmiö esiintyy. Tuo ylläeoleva alias ilmiö on niin ilmeinen että melko kokematonkaan ei tuohon ansaan helposti mene kun se on kerran tullut tutuksi. Tämä ei kuitenkaan toimi enää hyvin silloin kun ollaan nopeimmilla  vaakapyyhkäisyillä ja korkeilla signaalitaajuksilla. Tällä tavalla ei siis voi matkia suurilla taajuuksilla "Equal Time" toimntoa.  SDS1000X sarjassa ei ole E.T. toimintamuotoa. Mutta alhaisilla taajuuksilla se matkii sitä ihan mukavasti kuten kuva osoittaa.

On kuitenkin muita "kummajaisia" liittyen samaan asiaan ja niiden kanssa saattaa helposti olla enemmän ihmeissään.

Ennen seuraavia esimerkkejä on hyvä tietää se että olkoot oskilloskoopin samplenopeus mikä tahansa kuitenkin todellinen samplenopeus jolla ADC toimii on joko 500MSa/s kun kumpikin kanava aktiivisena tai 1GSa/s kun yksi kanava aktiivisena. Tarkoittaa sitä että jos säädät muistin ja/tai t/div asetuksen siten että samplenopeus on alempi otetaan AD muuntimelta samplemuistiin vain osa näytteistä (näyte=sample).
Jos skoopin ilmoittama "muistiin otettava samplenopeus" on esim 1MSa/s ja jos olisi 1 kanava aktiivisena toimisi AD muunnin  silti1GSa/s (niin on tässäkin kuvan tilanteessa) . 1MSa/s saadaan pudottamalla 999 samplea pois ja ottamalla 1 sample muistiin ja taas 999 tiputetaan pois ja seuraava siirretään muistiin edellisen perään jne. Näytenopeus muistissa josta näyttö muodostetaan on nyt 1MSa/s. 
Triggaus EI tapahdu tuosta muistista vaan AD muuntimen tuottamien triggausta ohjaavien näytteiden välit interpoloidaan ja siitä katsotaan tarkka ajallinen triggauskohta jonka perusteella näytölle piirrettävä vaakapyyhkäisy asemoidaan triggauskohtaan vaakasuunassa (ajallisesti). Se tietenkin johtaa siihen että ne samplet muistissa siirtyvät kuvassa mihin siirtyvät koska useinmiten näyte ei osu tarkalleen triggaustasoon vaan johonkin näytepisteiden välissä olevaan tasoon (joka kohta löytyy siitä näytepisteiden välille tehdyltä interpolaatio "viivalta" kohdasta jossa se leikkaa triggaustason). 

Jatketaan tällä kuvalla.
Usein oskilloskoopin käyttäjä on laittanut Sinc (Sin(x)/x) interpoloinnin pääle näyttömuotona "lines" (se on myös oskilloskoopin oletus asetus).  Signaali on 2kHz pulssi jonka leveys on 11,5µs. "Sampletaajuus" on 1MHz (1MSa/s) 
Siis, samplenopeus tarkoittaa sitä nopeutta jolla poimitaan samplemuistiin AD muuntimelta ulos tulevasta datajonosta. Oskilloskoopin näytöllä lukeva samplenopeus tarkoittaa sitä (vakiintunut käytäntö oskilloskoopeissa käytännössä aina).

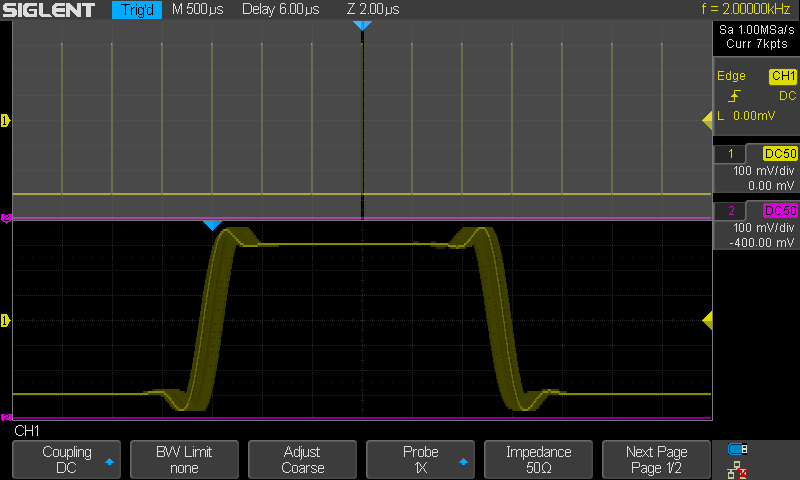
1 MSa/s riittää hyvin 2kHz signaalille - onhan sampletaajuus 500 kertainen. Tässä on kuitenkin "jekku".  

Sivuhuomautus: Tilanne olisi suhteellisesti ottaen sama jos samplenopeus olisi 1GSa/s ja pulssitaajuus 2MHz.

Jekku tässä on se että pulssireunojen nousu- ja laskuaika on 6ns. Tämä menee suhteellisesti niin överiksi että signaalin piirretyt nousu ja laskupaikat kokonaisuudessaan sattuvat sinne tänne yhden näytteenottovälin verran, kuten kuvasta näkyy. Kuitenkin ne lähes poikkeuksetta menevät siten että nousun kohdalla yksi piste on alhaalla ja seuraava täysin ylhäällä. Yhden näyteintervallin aikana koko askelmuutos.
Tuo EI ole triggausjitteriä (se selviää myöhemmin) vaikka se sille näyttääkin ja mittauksissakin käyttäytyy juuri niin. Voisi sanoa että tässä, vaikka triggaus olisikin kohdallaan tapahtuu piirtojitteriä. Tässä myös pulssin piirretty leveys vaihtelee saman verran, ei pelkästään sijainti. Lisäksi kuten huomataan Sinc interpolointi  aikaansaa jokaiseen nurkkaan ylilyönnin. Signaalissa sitä ei ole, eikä AD muuntimen datassa.


Seuraavassa kuvassa sama tilanne mutta nyt Sinc pois käytöstä ja näyttönä "lines" jolloin näytepisteet yhdistetään suoralla viivalla.

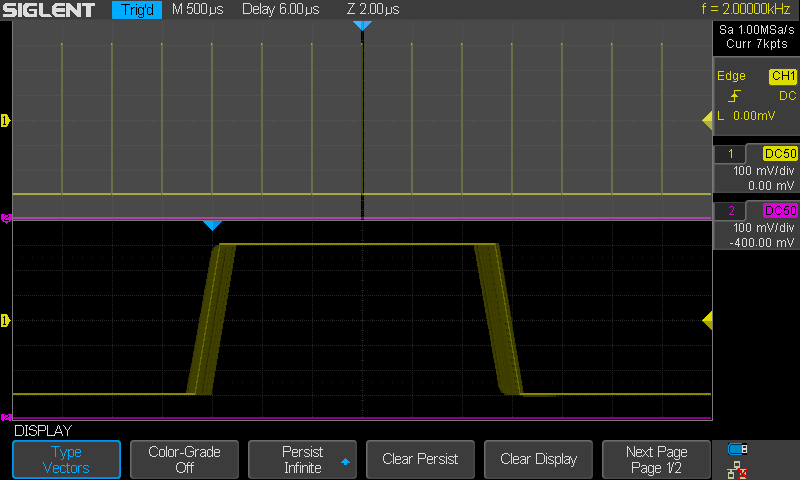
Kuvasta nähdään (koska persistence (jälkiloisto) on käytössä), että signaalin sijainti edelleenkin vaihtelee saman verran kuin Sinc ollessa käytössä. Vaihteluväli on kuvasta päätellen jokseenkin tarkasti 1µs. Tämä on näytepisteiden väli näytemuistissa.
Signaalin nousuaika on 6ns. Kuvassa yksikään samplemuistin näyte ei ole sattunut osumaan juuri johonkin keskelle sitä signaalin nousua. Datapiste on ollut joko signaalin alatasolla tai ylätasolla. Triggauksen interpolointi tietää paikan mutta kun kuvan piirtämistä varten ei ole olemassa kuin pisteet 1µs välein  on tuloksena tämä. Tuo on luonnollista. Tuon takia ei kannata alkaa uhrata resursseja ylimääräiseen triggauskohdan uudelleen interpolointiin kuvadatasta ja asemoimaan varsinkin kun tulos vaikuttaaisi ainoastaan  nousevan reunan viivaan ja muu saattaisi olla vieläkin ikävämpää.  Kauniin kuvan takia ei dataa kannata alkaa keksiä uudelleen, se olisi hiukan samaa kun  keksittäisiin hypoteesia tukeva data tutkimukseen tai otettaisiin huomioon vain sitä tukeva data. Tässä voisi keksiä dataa miellyttämään ihmisen silmän "odotuksia",  ainakin jos kyseessä olisi viihdelaite kauniita kuvia tuottamaan.



Tehdäänpä niin että ei yhdistetä datapisteitä millään viivalla. Todellisuudess ei tietenkään ole mitään viivaa. On vain yksittäisiä AD muuntimen tuottamia "pisteitä". Annetaan  skoopin piirrellä vain ne. Näyttötavaksi siis pisteet.

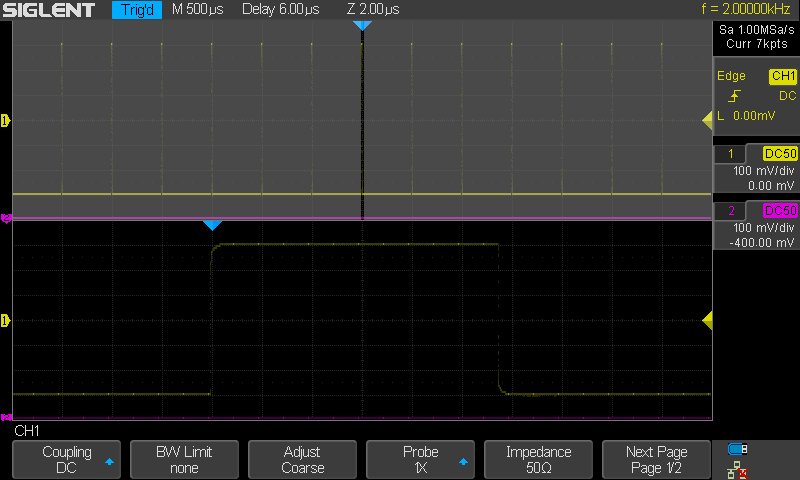
Hupsista. Vertaa edelliseen kahteen kuvaan. Signaali sama, kaikki muutkin asetukset samat, lukuunottamatta sitä, että pisteiden väliin ei interpoloida suoraa (lines) eikä käyrää (Sinc). Kirkkaat pisteet ovat ne datapisteet jotka tuli juuri siinä yksittäisessä vaakapyyhkäisysta mikä oli tehty ennen kuvan ottoa.

Näissä (pulssi kuvissa) olen valinnut käytöön Slow Acquisition jolloin TFT päivitys sisältää yhden vaakapyyhkäisyn jotta asia tulee selkeämmäksi ja näkyy kirkkaina vain yhden vaakapyyhkäisyn sample pisteet. Seuraavassa pyyhkäisyssa nuo pisteen olisi eri kohdassa ja kun odottaa niitä joskus sattuu myös niiden nopeiden nousevien reunojenkin kohdalle. Kuvassa on persitence päällä joten vanhat pisteen näkyvät myös koko siltä persitence ajalta. Uusimat näytölle kirkkaina ja vanhimmasta päästä pois.   Ei ole havaittavissa olevaa triggaus jitteriä. En ainakaan minä näe.
Edellisissä kuvissä olikin kuvan piirron aiheuttamaa "jitteriä".

Huomaa, että vaikka kuinka kauan jatkaisi tällä kuvan tavalla, pisteet osuvat aina tuolle samalle viivalle (ellei signaali muutu) ja tasavälien mutta ajallisesti satunnaiseen sijaintiin. Kanavan 2 vastaavat pisteen näkyvät myös ja koska AD muuntimet  käyvät rinnakkain ja samasta kellosta, niiden sijainti kanavan 1 kanssa on ajallisesti sama (täydessä synkronissa). 
Jos olisin kuvaa ottaessa valinnut Acquisition mode Fast  olisi kirkkaita  pisteitä enemmän koska yksi TFT päivitys sisältäisi nyt useita vaakapyyhkäisyjä (rriippuen signaaalista ja vallitsevasta wfm/s nopeudesta..
Jotta näissä esimerkeissä tilanne olisi selkeämpi, valitsin tuon "slow" toimintavan jota melko harvoin muuten yleensä käytetään. Kuitenkin sen olemassaolo kannattaa muistaa.
Dots, eli "piste" näyttötapaa kannattaa opetella hyödyntämään. Kaikkeen se ei sovi ja usein Sinc tai lines on ok. Joskus sen sijaan dots moodi on mainio.
Kuten tässä jos vertaat näitä kolmea yllä olevaa kuvaa.



Edellisissä pulssi signaalin kuvissa nousuaika pulssissa oli 6ns.  Näytteiden väli 1000ns. Ajatellaanpa että kyseessä on 100MHz oskilloskooppi jonka analogisen kanavan nousunopeus olisi 3.5ns ja näytteiden väli 1ns (kun 1GSa/s). 

Jatketaan asian tarkastelua käyttämällä näytteiden välinä edelleen 1000ns (1MSa/s).   Käytetään myös siihen nähden samalla suuruusluokalla olevia signaalin nousu ja laskuaikoja niin saadaan lisää käsitystä.

Aloitetaan kuvalla joka voi hämmästyttää tuon jitterin osalta. Huomaa erityisesti että triggaus on etureunasta.  Aiemmin sanoin että kyseessä ei ole triggaus jitteri vaikka se siltä kuvassa näyttikin. Nyt se todennetaan.

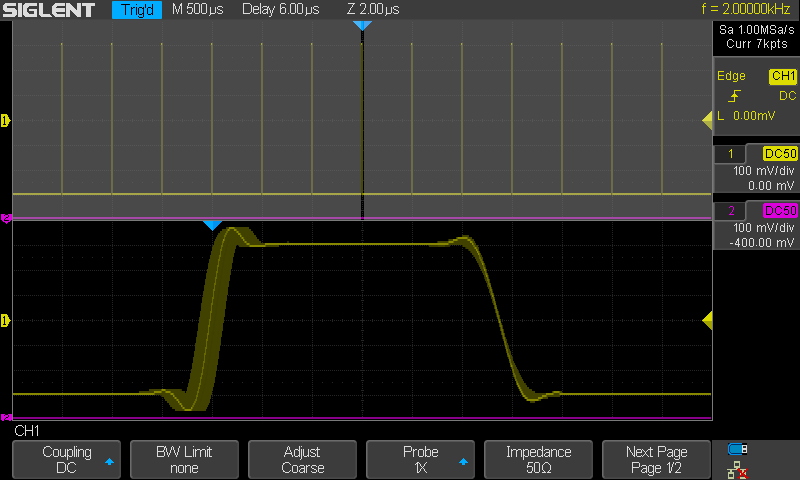
Kuvassa signaalin nousuaika on edelleen sama 6ns kuten aikaisemmin. Pulssin pituuskin sama 11.5µs.  Pulssin laskuajaksi olen asettanut 1500ns (1.5µs).
Triggaus on edelleen nousevasta reunasta ja kuvassa näkyvältä tasolta 0V.  Näyttömuotona "lines"  Interpolointitapa Sinc. Lisäksi persistence käytössä jotta kuvaan jää historiaa hiukan pidemmältä ajalta.  Jos kyseessä olisi triggausjitteri pitäisi tuolla laskevalla reunalla näkyä aikajitteriä koska triggaus on tuolla etureunassa. Eipä näy.  Etureunassa kuitenkin näkyy sama kuin aiemminkin. Triggaus itsessään siis on tarkka mutta etureunan kuvaan tulee aikajitteriä - tässä tapauksessa johtuen piirtämisesta - ei itse triggauksesta. Takareunan keskikohta jolla korkeudella triggaus on näyttää hyvin vakaaalta. Takareunassa ei tule "kuvan piirron" aiheuttamaa jitteriä koska sinne laskevalle reunalle saadaan aina kaaksi näytepistettä. (näytteiden väli 1µs ja laskuaika 1.5µs)

Sensijaan takareunassa edelleen näkyy jonkun verran alias ilmiötä signaalin nurkissa. Yksi aliasoinnin muoto on ns "corners wobbling".  Niin, samplenopeus on 1MSa/s ja laskuaika on 1.5µs.   Laskevan reunan tilanne vastaa saamaa kuin 1.5ns nousuaika samplenopeudella 1GSa/s (kun jätetään analogisen etupään osuus ennen AD muunninta pois vaikuttamasta). 

Seuraavassa sama ilman Sinc interpolaatiota.

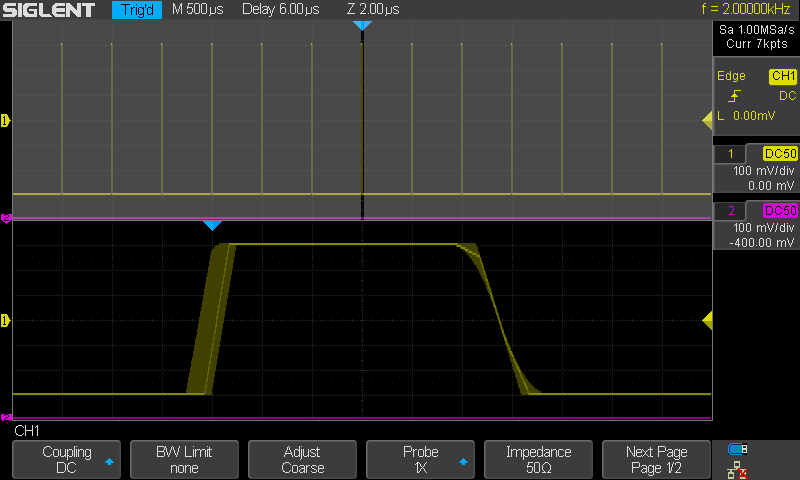
Kuvassa signaalin nousuaika edelleen 6ns sekä laskuaika 1500ns (1.5µs).  Sinc interpoloinnin aiheuttama nurkkien ylitys on poissa mutta muuten nurkkien "wobbler" jäljellä laskevan reunan nurkissa, kuten asiaan tietenkin kuuluukin. Tämä ei mitenkään liity valmistajaan vaan fysiikan ja matematiikan todellisuuteen. Noiden nurkkien "vipotus" ei näy still kuvassa mutta luveenähän nuo nurkat "vipottaa ja värisee".



Kurkistetaanpa miltä tilanne näyttää jos pitäydytään ainoastaan AD muuntimen tuottamassa datassa.

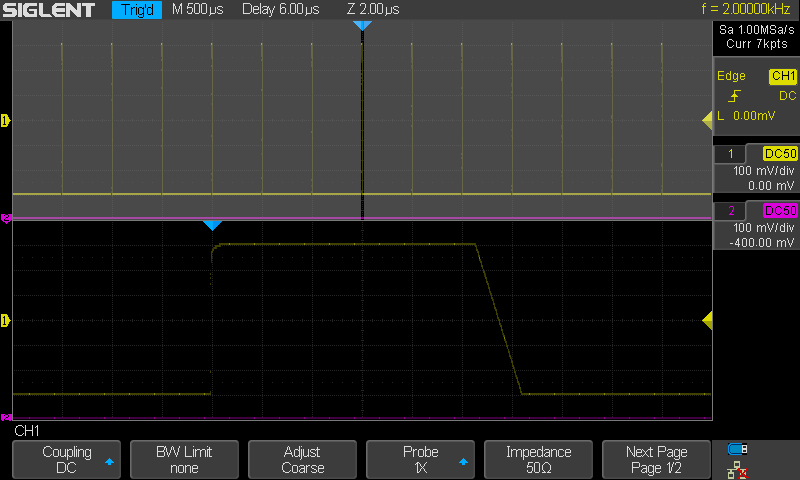
Ei vedetä viivoja pisteiden väliin. Ei Sinc interpoloituja eikä suoria viivoja.  Huomioi että yksi vaakapyyhkäisy on tuottanut ainoastaan noiden kirkkaiden pisteiden yhden jonon. Se että näet siinä signaalin muodon johtuu siitä että kuva sisältää ison joukon vaakapyyhkäisyjä koska persistence on käytössä ja edelliset pyyhkäisyt jäävät kuvapinnalle asetetuksi ajaksi. Voit mielessäsi kuvitella tuon edellisen kuvan syntymisen kun vedät viivat yhdistämään ajallisesti peräkkäiset kirkkaat pisteet. Sitten toistetaan sitä niin että kirkkaiden pisteiden jonon sijainti ajallisesti on siirtynyt satunnaisesti mutta samalla 1µs intervallilla ja taso on tuolla viivalla joka kuvaa signaalin muotoa. Satunnaisuus tulee ainoastaan siitä että signaalin ja AD muuntimen ajoituksen välillä ei ole yhteyttä.



Jotta tulee aivan selväksi se ettei kyseessä ole triggauksen jitteri vaan piirtäessä syntyvä aikajitteri esitän nuo kolme edellistä kuvaa hiukan "käännettynä".
Ensin Sinc, sitten lines ja lopuksi dots. Ero on vain siinä että nyt nouseva reuna on 1.5µs ja laskeva 6ns.  Muuten samat kommentit kuin edeltävissä kolmessa kuvassa.

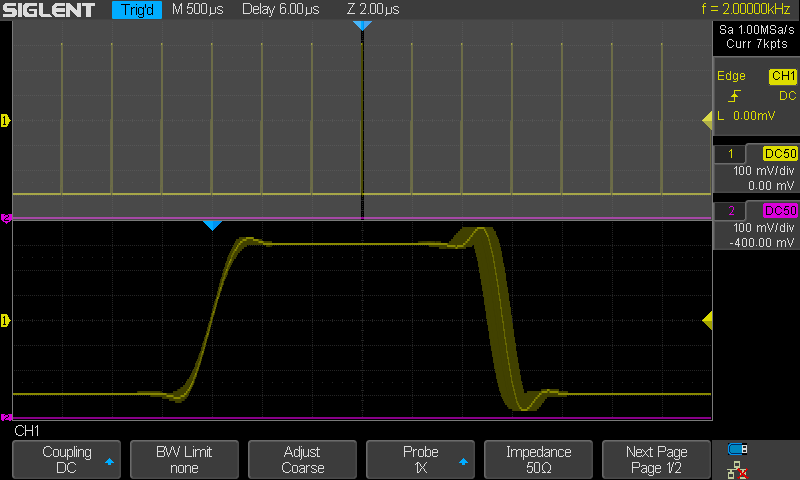
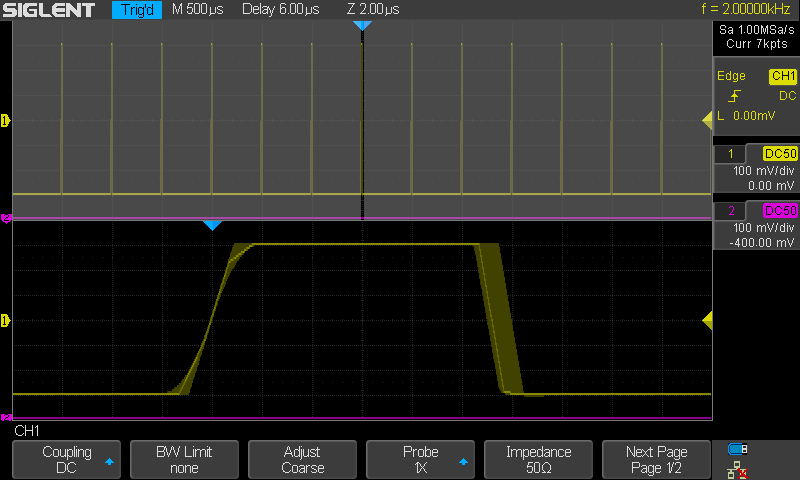
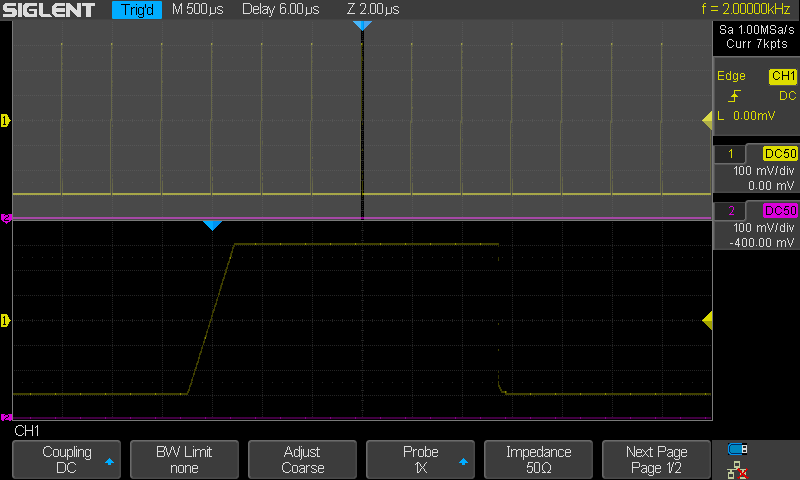
Edellisissä kolmessa kuvassa  nousuaika 1500ns ja laskuaika 6ns. Nämä edelliset kaikki 6 kuvaa yhdessä kertonevat selkeästi että tässä tapauksessa kyseessä on piirrettäessä syntyvä "jitteri" eikä suinkaan triggausjitteri. Triggaus toimii tarkasti mutta 1µs aikajitteri nopeisiin reunoihin tulee piirrettäessä koska piirrettäessä on käytössä vain 1µs välein olevat näytepisteet ja näytepisteiden väleille piirretään viivat jokaisella yksittäisellä vaakapyyhkkäisyllä. Mikäli taas näin ei tehtäisi vaan kerättäisiin usean vaakapyyhkäisyn pisteet lomittain oltaisiin aika lähellä ns Equal Time toimintamallia. Tapa jolla vaanhat digitaaliset osskilloskoopit toimivat. Esimerkiksi vanhan HP54501 oskilloskoopin samplenopeus oli maksimissaan 10MSa/s. Kuitenkin ns "repetitive" tilassa se kykeni helposti kuvaamaan 100MHz signaalia. Kunhan signaali oli ns jatkuva. Single shot "reaaliaika" oskilloskooppina se oli luokkaa 2 - 4 MHz. (huomaa kuitenkin että tässä käytetty "dots" näyttömoodi yhdessä persistence ajan  kanssa ei toimi samalla tavalla kuin joidenkin oskilloskooppien "Equal Time" toimintamuoto.)

Nyt jos esimerkiksi tuossa viimeisessä kuvassa signaalissa taapahtuisi merkitseviä  muutoksia sen ajan kuluessa jona samplepisteitä on kerätty näytölle (persistence aika) olisi kuva aivan toisenlainen "sotku" riippuen niistä muutoksista.


Seuraavaksi vielä muutama kuva joillain erilaisialla nousu- ja lasku ajoilla

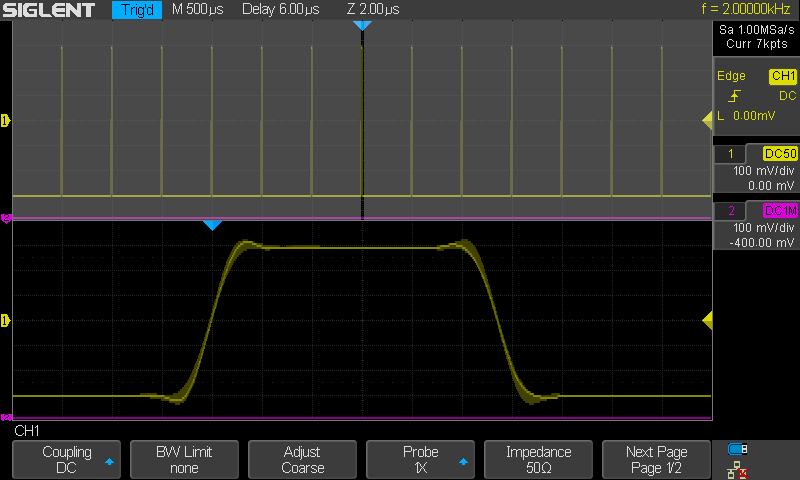
Nousu ja lasku 1.5 µs. Interpolointi Sinc

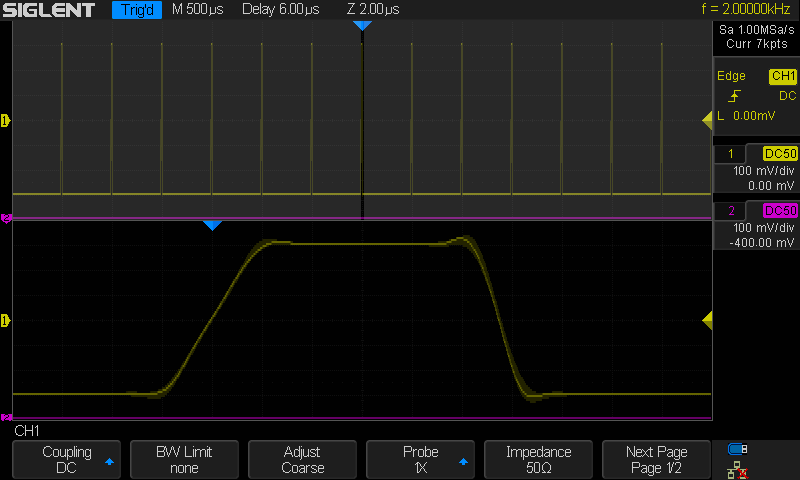
Nousu 3 µs ja lasku 1.5 µs. Interpolointi Sinc

Nousu 3.5 µs ja lasku 1 µs. Interpolointi Sinc

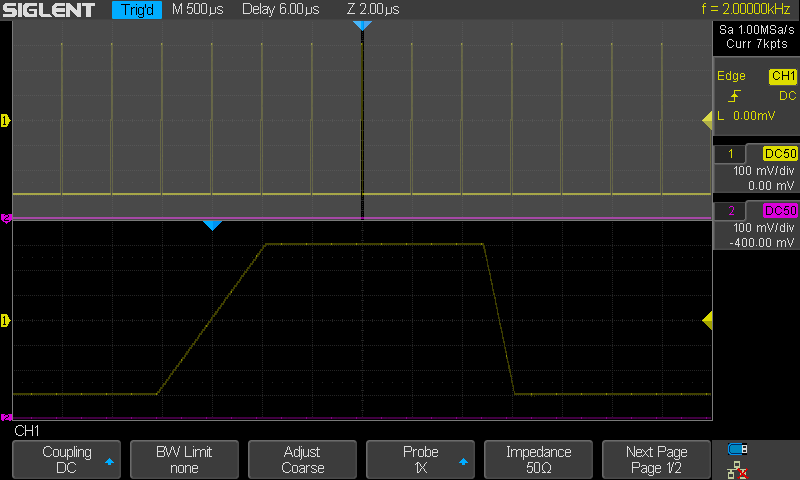
Nousu 3.5 µs ja lasku 1 µs.  Ei interpolointia. Vain pisteet. (ja persistence)



Seuraavaksi pieni kurkistus siihen miltä (puhdas) sini näyttää eri taajuuksilla.

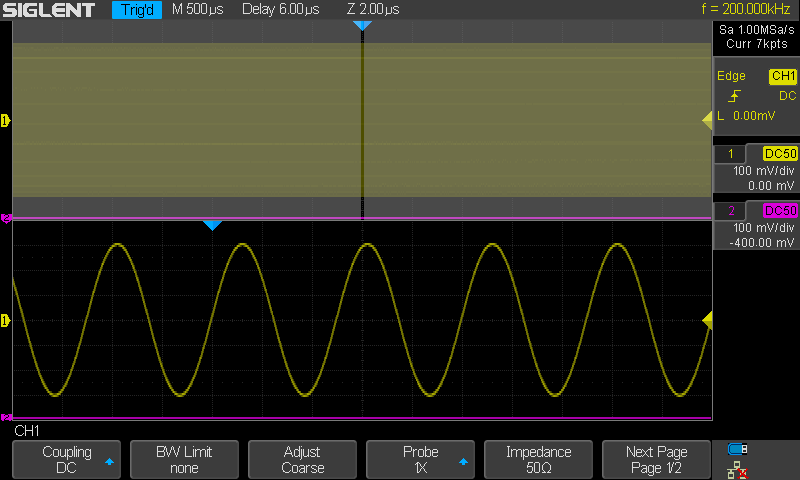
Kuvassa samplenopeus 1MSa/s ja taajuus 200kHz.  Tämä vastaisi samaa kuin 200MHz sini samplenopeudella 1GSa/s (kun etupään analogisen osuuden vaikutukset niillä taajuuksilla ei ole mukana. Eli tässä vaín tarkasteltuna se kuinka samplenopeus vaikuttaa.  Signaalin taajuus siis 1/5 sampletaajuudesta (1/2.5  Nyquist rajasta).
Näytön persistence on käytössä jotta nähdään mahdollinen vaihtelu eikä vain yhtä pysähtynyttä hetkeä (yhden kuvaruutupäivityksen väliseltä ajalta).  Persistence aika 10s.

.

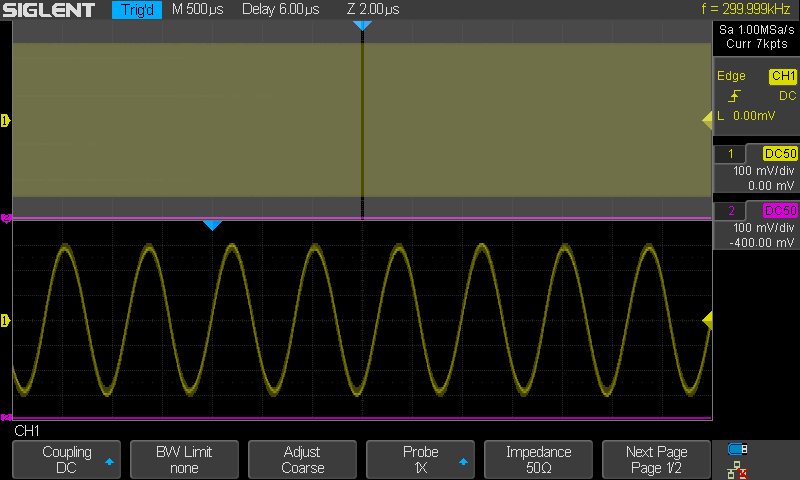
Kuvassa samplenopeus 1MSa/s ja taajuus 300kHz.  Tämä vastaisi samaa kuin 300MHz sini samplenopeudella 1GSa/s (kun etupään analogisen osuuden vaikutukset niillä taajuuksilla ei ole mukana).   Signaalin taajuus siis 1/3.33 sampletaajuudesta (1/1.67  Nyquist rajasta).  Näytön  Persistence aika 10s. Nyt aletaan nähdä signaalin huipuissa hiukan tason jitteriä ja aikatasossa havaitaan aivan juuri vaivoin erottuva vähäinen aikajitteri (piirrossa syntyvä, ei triggauksessa, vrt aiemmat kuvat). Kuvaa katsoessa huomioi mikä on todellisten näytteiden väli. Se on 1µs eli puoli ruutua!

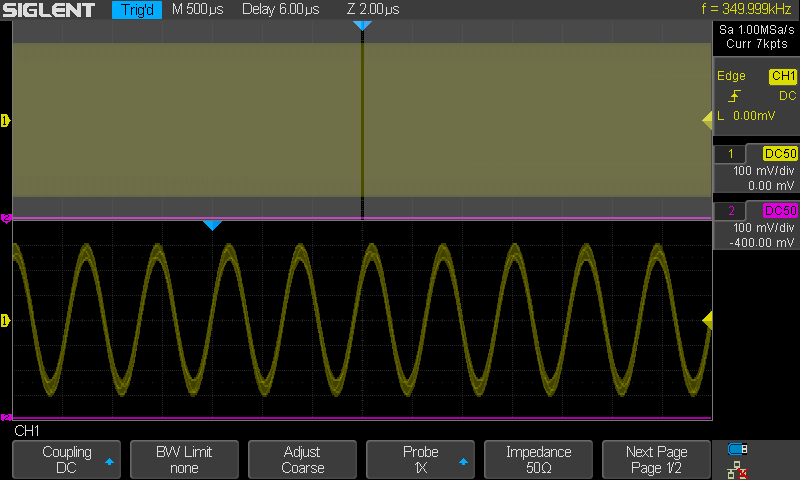
Kuvassa samplenopeus 1MSa/s ja taajuus 350kHz.  Tämä vastaisi samaa kuin 350MHz sini samplenopeudella 1GSa/s.  Signaalin taajuus siis 1/2.86 sampletaajuudesta. (1/1.43  Nyquist rajasta) Näytön  Persistence aika 10s. Nyt aletaan nähdä signaalin huipuissa taso jitteriä  kohtalaisen paljon. Nyt esiin tulee myös selkeästi kuvan piirron aiheuttama aikajitteri joka näyttää triggausjitteriltä. (ks aiemmat kuvat).  Kuvaa katsoessa huomioi mikä on todellisten näytteiden väli. Se on 1µs eli puoli ruutua!

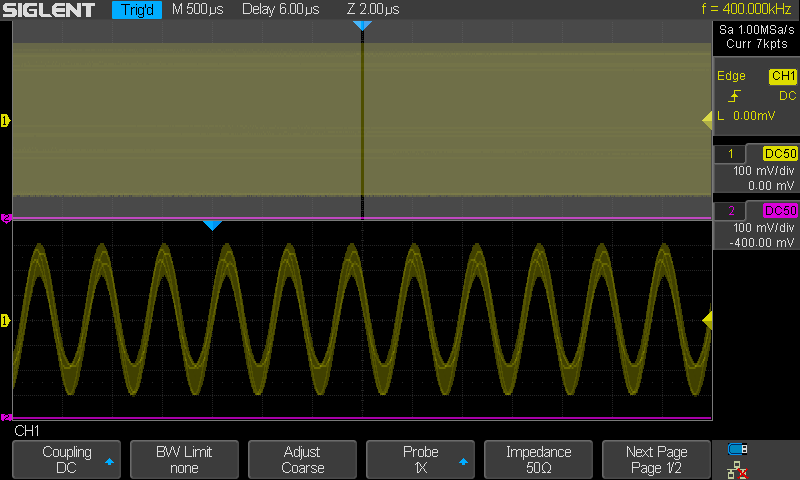
Kuvassa samplenopeus 1MSa/s ja taajuus 400kHz.  Tämä vastaisi samaa kuin 400MHz sini samplenopeudella 1GSa/s.  Signaalin taajuus siis 1/2.5 sampletaajuudesta. (1/1.25  Nyquist rajasta) Näytön  Persistence aika 10s. Nyt nähdään signaalin huipuissa taaso jitteriä  paljon. Jos nyt ajatellaan tuosta pois persistence osa ja katsotaan vain noita kirkkaita osia ja kuvitellaan että nähdään livekuvaa jossa nuo pomppivat jatkuvasti on meillä käsitys siitä miltä se näyttää.

Huomaa että tilanne luonnollisesti vastaa myös sitä tässä suhteessa sitä että samplenopeus olisi neljäs osa ja taajuus neljäs osa. 250MSa/s ja 100MHz. Onhan meillä näin edelleen jokin käsitys signaalista mutta on se aika kamalaa katsottavaa. Ajatellaanpa että sisään tulevassa signaalissa olisi korkempiakin taajuuskomponentteja mutta sellaisia joita emme tunne. Silloin voisi sanoa että yksi oskilloskooppi kuva valehtelee signaalista enemmän kuin tuhannella sanalla kykenisi puhumaan palturia.

Samplenopeuden ja signaalin taajuuskomponettien vaikutus on matematiikkaa. Siihen ei vaikuta oskilloskoopin valmistajan nimi millään tavalla. Siihen toki vaikuttaa esimerkiksi se millaisin parametrein Sinc interpolointi on toteutettu. Samoin asioihin joita näissäkin kuvissä näkyy vaikuttaa se kuinka hyvin triggaus  ja siihen liittyvä "hieno interpolointi" toimii. 


Moni on innostunut hakkeroimaan tai modifioimaan oskilloskooppiin lisää taajuuskaistaa (analogisen etupään taajuuskaistaa). Ikäänkuin taajuuskaistan leveys olisi jotenkin vain hyvä asia. Moni ei myöskään tunnista mahdollista ongelmaa joka siitä seuraa koska monilla ei ole minkäänlaisia välineitä eikä ehkä aina riittävää tietoa ja taitoa tutkia mitä se oikeasti vaikuttaa.

Muistutan vielä kerran: Oskilloskoopilla analysoidaan signaalia joka on enemmän tai vähemmän tuntematon. Muussa tapauksessa analysoimme oskilloskooppia.

Jos emme tunne oskilloskoopin ominaisuuksia (emmekä signaalin ominaisuuksia) on aivan turha puhua signaalin tutkimisesta. Silloin sensijaan olemme "ihmettelemässä ihmeellisiä ilmiöitä joita skoopin kuvaruudulla näkyy"  ja se on lähinnä  viihdettä joskin sekin voi olla mielenkiintoista ja opettavaistakin - jos ottaaa opiksi..

Nykyaikana onneksi oskilloskoopeissa alkaa olla näytemuistia kohtuullisen reilusti.  Tämäkin on yksi tärkeä seikka. Myös alias ilmiön kannalta.
Siglent SDS1102X samplemuistin pituus on max 14M kun yksi kanava on käytössä. Tai 7M  kummallkin kanavalle samaan aikaan. Vastaavasti maksimi samplenopoeus 1GSa/s kun yksi kanava on käytössä ja 500MSa/s kun kaksi kanavaa käytössä.  Tästä seuraa se että  koko vaakkapyyhkäisyn nopeusalue 1ms/div  - 2ns/div voi käyttää 1GSa/s (tai 500MSa/s kun kaksi kanavaa käytössä).  Kun oskilloskoopissa on hyvin pieni näytemuisti joutuu oskilloskooppi pudottamaan hyvin nopeasti näytenopeutta kun vaakapyyhkäysyn nopeutta lasketaan. Ja, kuten on selvää, matalalla  samplenopeudella myös Nyquist raja tulee vastaavasti alemmas.

Jatketaan ja töydennetään myöhemmin....
To be continue...

--»  Ylös 

--»  Oskilloskoopit

--»  Etusivulle - Home