Oskilloskoopin Sin(x)/x interpoloinnista

Perustietoja Siglent oskilloskooppien interpoloinnista ja näyttötavoista

Kesken. Kuitenkin jotain hyödyllistä jo tässäkin joten...

Tämä liittyy hyvin läheisesti myös toiseen esitykseen jossa enemmän asiaa alias ilmiöstä digitaalisissa oskilloskoopeissa.
On mahdollista että joskus yhdistän ja muotoilen nämä kaksi yhdeksi kokonaisuudeksi ja "harmonisoin" hiukan ilmaisuja.
Se kannattaa lukea yhdessä tämän kanssa.

Oheismateriaalina kannattaa myös lukea: Sin(x)/x Interpolation: An Important Aspect of Proper Oscilloscope Measurements
By Chris Rehorn, Agilent Technologies

Esimerkeissä käytetyt laitteet:
 
Digitaalinen oskilloskooppi Siglent   SDS1204X-E
Analoginen oskilloskooppi   Tektronix 2465ADM
Signaaligeneraattori        Siglent   SDG1032X
Spektrianalysaattori        Siglent   SSA3032X


Digitaalisessa oskilloskoopissa tulosignaalin AD muunnoksen jälkeen on jono yksittäisiä peräkkäisiä näytepisteitä. Näytepisteiden aikaväli riippuu oskilloskoopista ja käyttäjän tekemistä valinnoista. Usein ei haluta katsella pelkkiä pistejonoja näytöllä vaan halutaan että niistä muodostuu signaalia (mahdollisimman hyvin) kuvaava yhtenäinen viiva samaan tapaan kuin analogisissa oskilloskoopeissa se tapahtuu luonnostaan.  Yhtenäinen signaalia kuvaava viiva voi muodostua monin tavoin. Mikäli peräkkäin on hyvin tihessä AD muuntimen tuottamia datapisteitä ne muodostavat viivan jo sellaisenaan. Hyvin usen on kuitenkin tilanne toinen varsinkin jos signaalin muutosajat ovat lyhyitä verattuna näytevälin pituuteen.


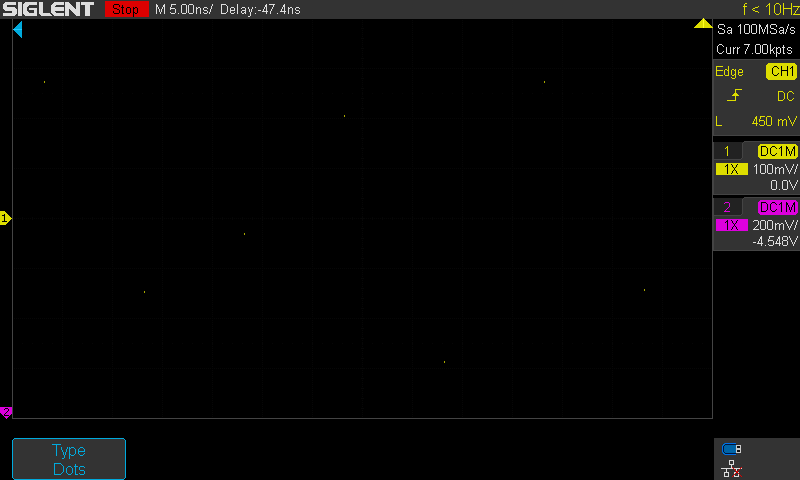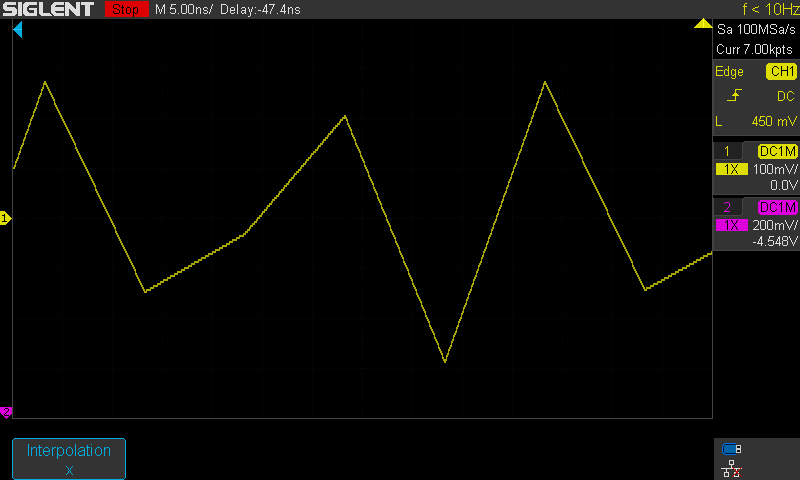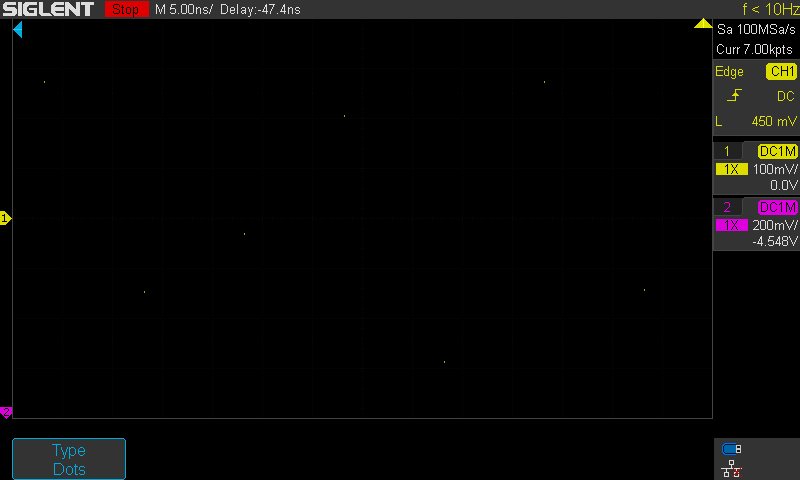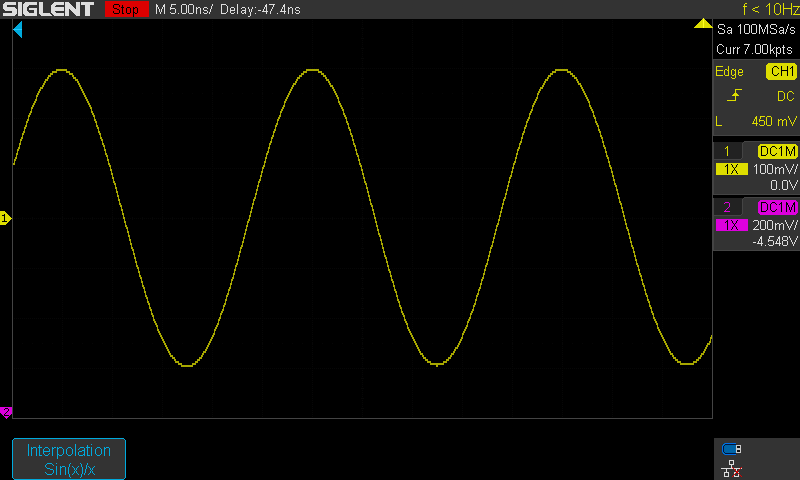
Kuva A on GIF animaatio jossa peräkkäin täsmälleen samasta signaalin näytedatasta näyttö: dots--vectors--dots--Sin(x)/x ja toisto.
Tässä nähdään myös kuinka Siglent Sin(x)/x ei riko sääntöjä ja tulos kulkee todellisten näytepisteiden kautta.
Kuvassa signaalina 40MHz puhdas siniaalto, 5ns/div (ruudut himmennetty jotta pisteet erottuu tässä selvemmin. Näytenopeus on tarkoituksellisesti alhainen 100MSa/s jollon tutkittavan siniaallon taajuus 40MHz vastaa 0,8*fNyquist. jota pidetään sopivana maksimina yleisesti tämän tyyppisille oskilloskoopeille Sin(x)/x interpolaatiota käytettäessä.





Kuva B on GIF animaatio jossa peräkkäin täsmälleen samasta signaalin näytedatasta näyttö: dots-vectors-dots-Sin(x)/x.
Tässä nähdään myös kuten kuvassa A kuinka Siglent Sin(x)/x ei riko sääntöjä ja tulos kulkee todellisten näytepisteiden kautta.

Sen sijaan itse signaali rikkoo tässä todella pahasti sääntöjä. Signaalissa esiintyy paljon fNyquist (nyt 50MHz) ylittäviä taajuuskomponentteja (nousuaika) jotka muodostavat aliaksia jotka näkyisivät pahasti signaalin nurkkien edestakaisena ajallisena ja tasollisena hyppelynä mikäli oskilloskooppi olisi Run tilassa.
Tämän lisäksi näkisimme että triggaus jitteri olisi kasvanut katastrofaaliseksi. Koko signaalin nouseva reuna mahtuu näytteiden väliin ollen noin vajaa puolet näytevälistä. Näyte voi osua juuri nousevaan osaan tai jonnekin muualle ja nousevasta reunasta ei enää saada luotettavaa ajallista sijaintia näytteisiin nähden. Peräkkäisten vaakapyyhkäisyjen aikajitteri triggaustasolla olisi yli 5ns.
Tässä kyseisessä tapauksessa triggauksen aikajitteri olisi  lähes näkymätöntä mikäli tulevan kanttiaallon nousuaika olisi suurempi kuin noin 11-12ns.
(huom: kuvassa B näkyvä nousuaika ei ole signaalin vaan sen määrää nyt enemmänkin näyteväli ja Sinc interpolointi)

Huomaa että kuvan tilanteet animaation kunkin näyttöruudun osalta on pysäytettyjä ja pohjautuu täsmälleen samaan ADC dataan (joka näkyy kun vain todelliset pisteet (dots)). Näin on saatu esiin se että Sinc interpolointi todellakin piirtää oikein näytteisiin nähden mutta vain niihin nähden. Signaalistahan se ei tiedä mitääjn muuta. Ei se tiedä jos signaali rikkoo interpoloinnin sääntöjä  kun on tulosignaalista AD muuntimen näkemän signaalin taajuuskomponentteihin nähden alinäytteitetty.

Oskilloskoopin käydessä (Run) tilanne dots näyttötavalla näyttää erilaiselta. Kulloisestakin wfm/s nopeudesta riippuan päällekkäin kerrostetuna voi olla suuri määrä tällaisia yksittäisiä kuvia ja kun ADC ei toimi synkronissa tutkittavan signaalin kanssa niin esim pisteitä näkyisi huomattavastikin enemmän riippuen asetuksista ja signaalista.

On luonnollista että se mitä useinmiten käytetään ja joka usein on oskilloskoopissa oletusarvona valittu käyttöön on Sin(x)/x interpolointi. Hyvin usein, mutta ei ihan aina, paras tapa yhdistää nuo pisteet on käyttää Sin(x)/x interpolointia (Sinc) joka on sekä teoriassa että käytännössä oikea tapa mikäli eräät ehdottoman tärkeät ehdot täyttyvät. Niistä myöhemmin. Toinen tapa yhdistää pisteet on vetää suora viiva pisteiden väliin (Line tai Vector usein nimenä). Kun näyteväli on suhteellisen harva signaalin taajuuteen nähden tulos on varsin kehno. Sensijaan jos näyteväli on erittäin lyhyt suhteessa signaalin muutosnopeuksiin tulos on luonnollisestikin hyvä.

Jos jotain pitää näistä tavoista sanoa niin Sin(x)/x (Sinc) on parhaimmillaan kun aaltomuodot ovat siniaaltotyyppisiä vaikka olisivatkin monipuolisia monimuotoisia. Joissan tapauksissa se ei ole aivan optimaalinen ja suora viivakin saattaa olla soveliaampi. Tällöin on kuitenkin usein tilanne se että on puutteita Sinc interpoloinnin kaikkien ehtojen toteutumisessa joka onkin käytännössä erittäin usein tilanne varsinkin pulssi-kantti tyyppisillä signaaleilla. Siksi voi sanoa että suora viiva (line) voi joskus olla edullisempi näillä kanttialloilla ja kun toimitaan oskilloskoopin ylärajoilla. Pääsääntöisesti Sinc sopii kaikeen. Joissain tilanteissa erityisesti pulssi-kantti typpisille signaaleille suora viiva (Line) voi olla kokeilemisen arvoinen varsinkin jos epäilee että Sinc interpolointi tuottaa ylilyöntiä liittyen pulssireunoihin (Gibbs ilmiö), samoin kuin jopa myös pelkkien pisteiden käyttö. Se ei paljoan maksa kun kokeilee kaikkia kolmea vähänkään epäilyttävissä tilanteissa ja päättelee niiden pohjalta.

Sin(x)/x interpolointi edellyttää ehdottomasti oikein toimiakseen: (ja tämä usein unohdetaan)

1. Tutkittavasta signaalista ei saa päästä AD muuntimelle taajuuskomponentteja jotka ylittää taajuuden: Näytetaajuus/2 joka tunnetaan  nimellä  fNyquist  (Nyquist-Shannon  teoreeman mukaisesti)
Lisähuomautus: Käytännössä ideaalia Sinc rekonstruktiota ei voi oskilloskoopissa toteuttaa ja siksi on hyvä pysyä alle ~0,8*(näytetaajuus/2)

2. Näytevälien tulee pysyä samana. Yleensä toteutuu tällaisissa oskilloskoopeissa riittävän hyvin.

Sinc interpoloinnin sääntöjä ei kovin helposti riko oskilloskoopilla mikäli sen maksimi näytenopeus on 1GSa/s ja kaistanleveys 100MHz.
Niin voisi helposti luulla. Se on totta silloin kun oskilloskooppi myös käyttää maksimi näytenopeuttaan.
Aina ei niin kuitenkaan ole. Ja se tulee ottaa huomioon.

Usein jos sellaisessa 100MHz oskilloskoopissa on useampi kanava samaan aikaan käytössä näytenopeus putoaa riippuen rakenteesta. Samoin mikäli käytetään hitaampia aikoja (t/div) jolloin oskilloskoopin on pudotettava näytenopeutta sen mukaan mikä on mahdollista vallitsevalla t/div asetuksella ja vallitsevalla muistin pituudella. Voihan olla että esimerkiksi muisti ei rajoita näytenopeutta vallitsevalla t/div asetuksella mutta on otettu kaikki 4 kanavaa käyttöön ja näytenopeus on vain 250MSa/s (Esim Rigol DS1000Z) tai 500MSa/s (Siglent SDS1?04X-E) Samoin näytenopeutta joudutaan alentamaan hitaammilla t/div asetuksilla kun muistin pituus alkaa rajoittaa sitä joko maksimi muistin tai käyttäjän asettaman maksimi muistin rajoittaessa.

Seuraavassa muutama esimerkki. Esimerkkikuvissa signaalina on noin 40ns mittainen pulssi taajuudella 1,87MHz
Huomaa että kaikissa alla olevissa 40ns pulsssin kuvissa on täsmälleen sama signaali oskilloskoopin sisääntulossa.
Signaali tulee 50ohm koaksiaalikaapelilla generaattorilta ja oskilloskoopin päässä 50ohm impedanssi.


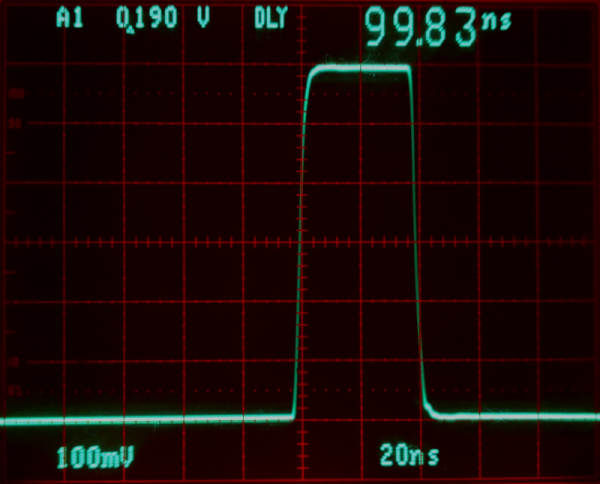
Kuva 1.
Analogisessa oskilloskoopissa ei synny erilaisia alias ilmiöitä eikä "Gibbsin korvia" kantin nurkkiin joita mitään ei oikeasti tutkittavassa signaalissa ole. (Tässä oskilloskooppina Tek 2465ADM)




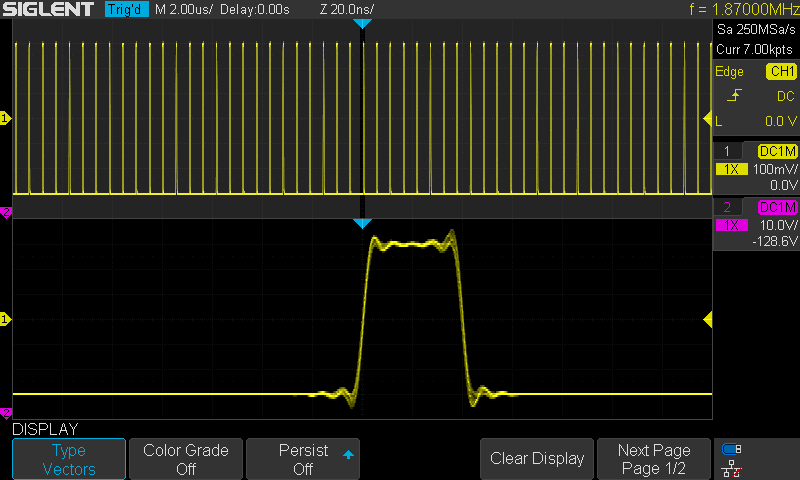
Kuva 2.
Oskilloskoopissa Sin(x)/x joka toteutuu vain jos näyttömuodoksi on myös valittu vectors. Jos tässä vectors näyttömuodossa kytketään Sin(x)/x interpolointi pois silloin pisteet yhdistetään suoralla.
Oskilloskoopin aika ja muisti asetukset on tarkoituksellisesti valittu siten että näytenopeus on saatu pudotettua 250MSa/s. Käytössä siis kanavaparin 1 molemmat kanavat ja muisti rajoitettu 7k sekä aika asetus 2us/div jolloin saadaan pudotettua 250MSa/s. Jotta on saatu sitten 20ns/div on käytetty ikkunoitua zoomausta jossa nyt 5 näytettä/div. Näyteväli 4ns on melko lähellä signaalin todellista nousu ja laskuaikaa. Kuvassa signaalin "nurkissa" näkyy oikein mainiosti Gibbs ilmiö "Gibbsin korvat" - "Gibbs ears" ja siis niitähän ei oikeasti todellisessa sisään tulevassa signaalissa ole.



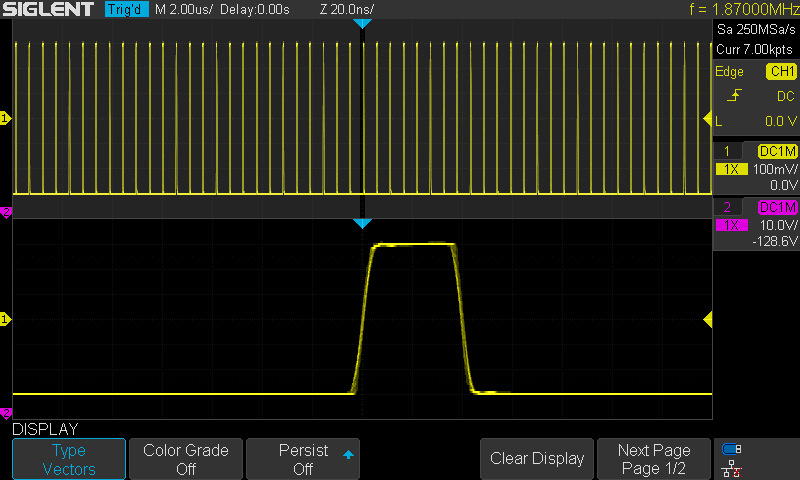
Kuva 3.
Kuten kuva kaksi mutta Sin(x)/x kytketty pois jolloin lineaarinen eli suora viiva pisteiden väliin. Huomaa että Gibbs ilmiö katoaa. Sensijaan jos signaalissa olisi esim overshoot todellisuudessa silloin se näkyisi myös tässä!
Tämä on syy miksi joskus suositellaan pulssi-kantti tyyppisille signaaleille tätä interpolointitapaa tai ainakin epäilyttävissä tilanteissa kokeilemaan sitä ja tulkitsemaan sitten eron perusteella tilannetta. Luonnollisesti toisen ja vielä parempi tapa on kasvattaa näytetaajuutta mikäli se suinkin on mahdollista. Huomaa että vaikka tässä on käytetty melko alhaista näytenopeutta (250MSa/s) niin tämä kuitenkin sakaalautuu jokseenkin suoraan. 500MSa/s tapahtuu aivan samaa mikäli nousuaika alkaa olla lähellä 2ns ja vastaavasti alaspäin. Sama ilmiö.



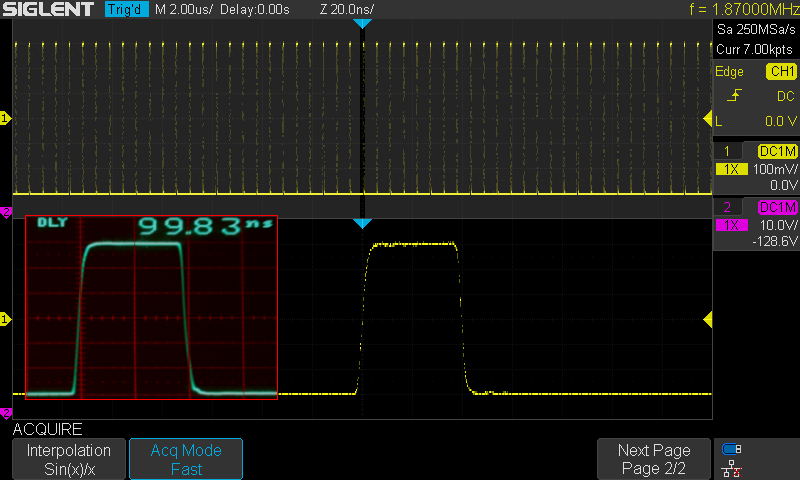
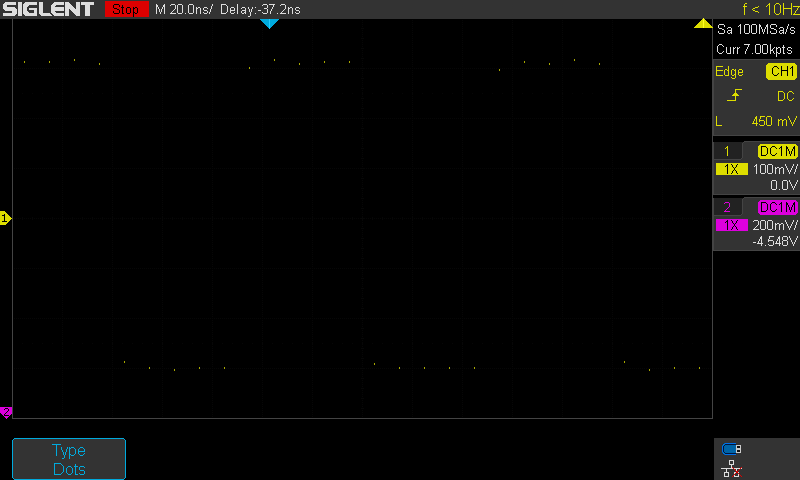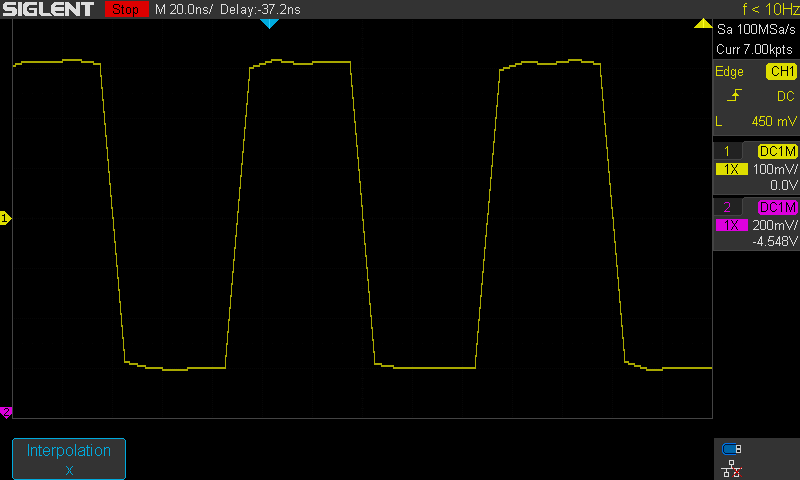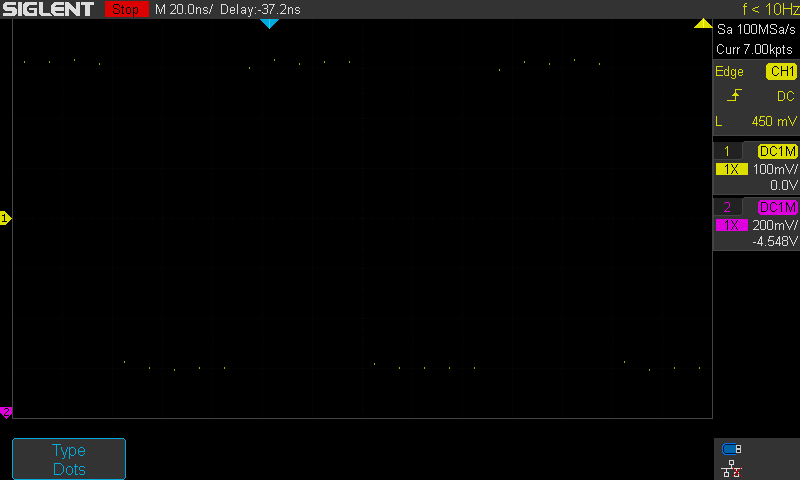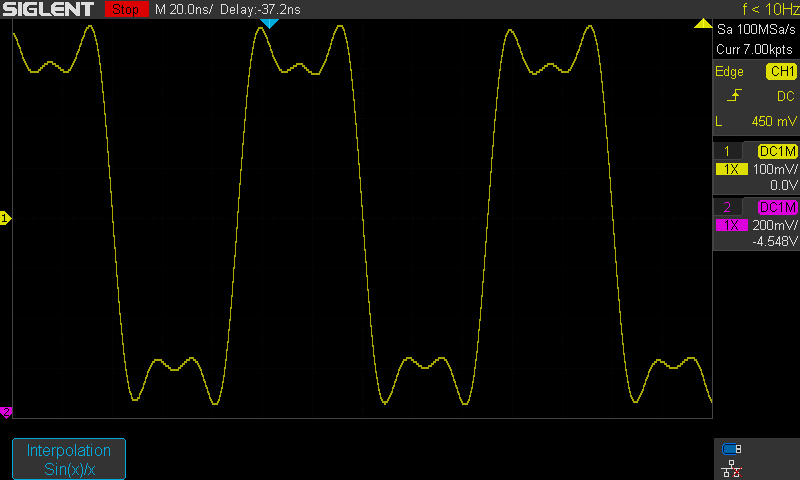
Kuva 4.
Tässä interpolointia ei tehdä. Vaikka valittuna onkin Sin(x)/x niin näyttömuodoksi on valittu pisteet (dots) joka ohittaa interpoloinnin ja kuvaan tulosteaan vain todelliset ADC näytepisteet. Koska tälläkin asetuksella oskilloskooppi on kohtalaisen nopea on kuvassa pisteitä paljon enemmän kuin yksi jokaista 4ns kohden. Mikäli Acq mode Fast (oletus) halutaan pudottaa on jokaisessa TFT kuvan päivityksess avain yksi vaakapyyhkäisy ja siis yksi näytejono. Nopeassa moodissa jokainen TFT kuva saattaa sisältää useita peräkkäisiä vaakapyyhkäisyjä kerrostettunna. Pisteiden aikasijainti on kussakin vaakapyyhkäisisyssä satunnainen koska tutkittavan signaalin ja ADC kellopulssin välillä ei ole mitään synkronointia tietenkään. TFT päivitysväli on luokkaa 40ms. Kerrostettuna on ne vaakapyyhkäisyt jotka on sinä aikana ehditty suorittaa. Nopeuden määrää toisaalta signaali ja toisaalta oskilloskoopin nopeus johon se enintäöän kykenee kulloisillakin asetuksilla.
Useissa tilanteissa varsin käyttökelpoinen mikäli interpolointi ei jostain syystä ole optimaalinen.
Koska ihmisen silmä on hiukan hidas ja aivot rekonstruoi kuvaa näyttää tilanne livenä paremmalle kuin tuossa pysäytyskuvassa koska aivot yhdistää niitäkin TFT frameja jotka se juuri näki. Tämä on täsmälleeen yksi frame. Kuten havaitaan tässä tilassa signaalin muoto vastaa varsin hyvin sitä kuinka 300MHz hyvä analoginen oskilloskooppi sen näkee.  Samoin edllinen Kuva 3.  Vain Sin(x)/x interpolointi tuotti vireheellisen kuvan signaalista (Kuva 2.).



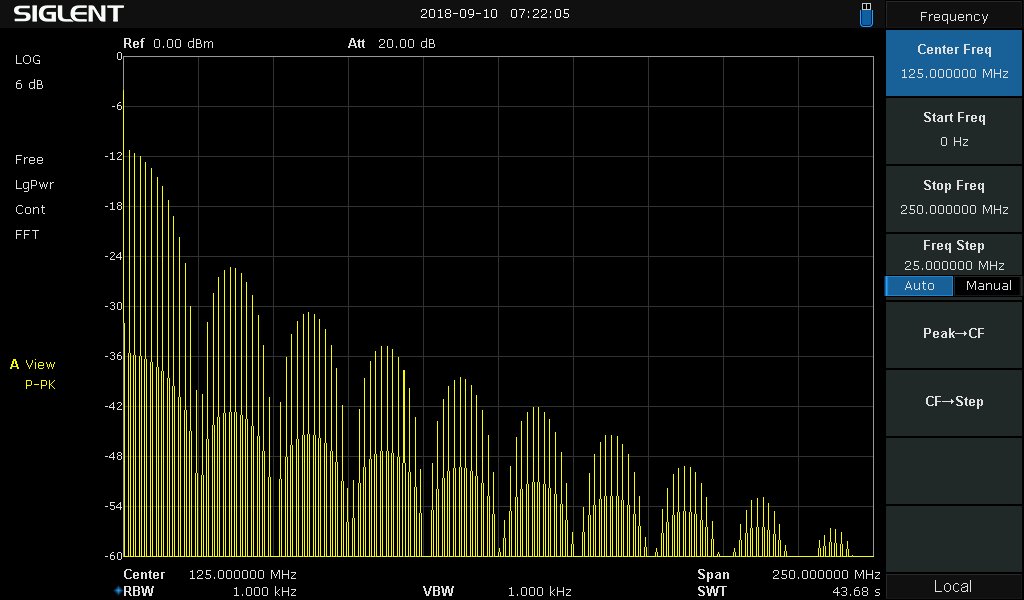
Kuva 5.
Sama signaali kuin kuvissa 1. - 4.
Mikäli oskilloskoopin näytetaajuus on 250MHz on fNyquist 125MHz, kuvassa keskellä. Oskilloskoopissa voi ajatella nyt tapahtuvan niin että taitetaan tuo kuva tuosta 125MHz keskilinjalta ja siitä ylöspäin olevat taajuudet taittuvat tuohon päälle taakaisin päin. Niin se vaan toimii. (itseasiassa tuo "fold back" ajattelu helpottaa usein. Jos fNyquist olisi esim 50MHz niin siitä vaan taittelemaan kuvaa. 50 kohdasta taaksepäin ja taas nollakohdasta ylöspäin ja edelleen 50 kohdasta taaksepäin jne...sen taitellun haitarin läpi kun katsoo niin näkee missä kukin taajkuus on tuossa 0-fNyquist peruskaistalla. (tokihan sen voi laskeakin. Mutta laskukaava ei aina hahmota asiaa "kuvaksi" mielessä.)
Kuvaa katsoessa tulaa huomioida se että oskilloskoopin ADC näkisi tilanteen noin ainoastaan mikäli analogisen tuloasteen kaistaleveys olisi rajoittamaton ja tasainen. Se etupään vaimennus luonnollisesti vaikuttaa (ja estää aliasointiakin). Kun oskilloskoopin ADC on täydellä skaalalla 8 bittiä on sen teoreettinen dynamiikka alue 48dB. Käytännössä se ei ole niin paljon. Yleensä et oskilloskoopissa myöskään käytä täyttä skaalaa vaan enintään noin 80% koska näyttö on kahdeksan ruutua korkea mutta täysi ADC lukualue 256 tasoa on hiukan yli 10 ruutua. (lineaarisuus siellä reunoilla ei ole kovin hyvä joka ei johdu AD muuntimesta vaan analogisesta asteesta ennen sitä.)  Analogisissa oskilloskoopeissa sen lisänä oli kuvaputken poikkeutuksen virheet. Mutta edelleen kannattaa noudattaa vanhaa sekä HP että Tektronix ohjetta että esimerkiksi oskilloskoopin kaiataleveys mitataan 6 ruudun korkuisella signaalilla. Eipä siitä ole syytä luopua ja itse käytän yleeensä aina sitä.

Sen lisäksi oskilloskoopissa Sin(x)/x ei suinkaan ole täydellinen jo siksikin koska eihän sitä voi laskea äärimmaisen pitkästä datajonosta vaan muutamaan näytteen yli. Se tuottaa omat "ilmiönsä" jo hiukan aiemmin... tuolla 100MHz tienoilla jo havaittavana. Pitää myös aina muistaa että kun puhutaan näistä taajuuksista, olkoon se sitten kaistaleveys tai Sinc interpolointi tms, niin puhutaan siniaallosta. Tuossa spektrikuvassa on piikki jokaisen sinialalon kohdalla josta tuo oskilloskoopin sisääntuleva pulssi voidaan ajatella koostuvan. Jotta alkuperäinen signaali ei vääristy on oskilloskoopin pystyttävä toistamaan nämä jokainen siniaalto tasoltaan alkuperäisenä. Jos (kun) näin ei ole, oskilloskooppi vääristää signaalia (enemmän tai vähemmän).





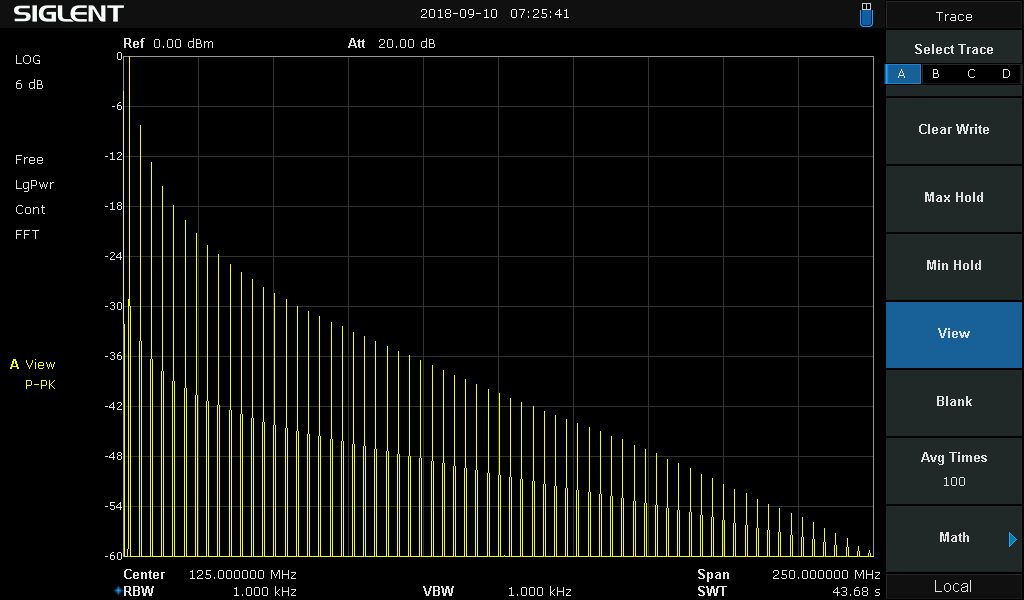
Kuva 6.
Mikäli signaali olisi tuolla samalla taajuudella 1.87MHz tuon lyhyehkön pulssin sijasta kanttiaaltoa näyttäisi sen koostumus tältä. Siinä on melkoinen joukkio siniaaltoja jotka kaikki oskilloskoopin olisi toistettava mitään taajuutta korostamatta tai vaimentamatta jotta kuva vastaisi signaalia. Toki tuo vielä jatkuisi pidemmällekin mutta humataanpa että oskilloskoopin AD muunnin on 8 bittinen. Teoriassa siis dynamiikka 48dB jos AD muunnin olisi ideaali. Kuvassa 6dB ruudut joten 8 ruutua vastaa 8 bitin lukualuetta. (kuvassa kantin perustaajuus eli 1. harmoninen on trasoltaan hiukan yli 1dBm. (niin sain tuon asteikon "nätiksi" 0 - 60dB ja koska tarkoitus on vain esittää periaatetta))
Tässä kohden on hyvä ajatella. Jos sama kantti olisi vaikkapa vain 1kHz taajuudella mutta sama nousuaika, silloin noita yksittäisiä siniaaltokomponentteja olisi huomattavasti tiuhempaan. Oskilloskoopin (SDS1204X-E) analogisen etupään kaistaleveys ennen AD muunninta on nimellisesti 200MHz mutta toki se jatkuu siitä ylöspäin hiljalleen vaimentuen. Jos näytetaajuus on 1GHz on Nyquist rajataajuus 500MHz. 500MHz näytetaajuudella 250MHz ja 250MHz näytetaajuudella 125MHz jne. Kaikki mitä AD muunnin "näkee" ja joka ylittää kulloisenklin Nyquist rajataajuuden generoivat aliaksia.



Jotta välttää ongelmat ja pahasti virheelliset tulokset on digitaalisen oskilloskoopin käyttäjän oltava ainakin auttavasti perillä näistä asioista ja tietää edes jotain siitä millä tavoin virheet usein ilmenee ja millä yksinkertaisilla keinoilla niitä voi välttää tai tarkistaa onko ehkä sellaisesta kyse. Niitä kannattaa harjoitella jolloin niistä kokemuksen myötä tulee rutiinia ja silmä oppii ne seikat jolloin pitää epäillä näkyvää signaalin kuvaa ja lähes automaattisesti tulee tehneeksi pari pikku asetusmuutosta joiden avulla epäily joko vahvistuu tai vaimenee.
Joka tapauksessa aina pitää ymmärtää että oskilloskoopin kuva on aina virheellinen, enemmän tai vähemmän.

Muutama perus vinkki alias ilmiöiden sekä interpoloinnin tuottamien normaalien mutta joskus haitallisten ilmiöiden eliminoimiseksi.

1. Käytä Sin(x)/x interpolaatiota oletusarvoisesti mutta käytä myös muita tapoja jotta niiden käyttö pysyy ns "lihasmuistissa". Mikäli haluat sen vaikutuksen pois tilapäisesti vaihda näyttömuodoksi "Vector" sijalle "Dots".

2. Pyri aina käyttämään maksimaalista näytenopeutta. Sen turvaa parhaiten valitsemalla muistin maksimipituudeksi oskilloskoopin maksimi kun toimitaan alemmilla vaakapyyhkäisynopeuksilla. Ellei jokin erityinen seikka ole syynä muistin pituuden rajoittamiseen. (esimerkiksi sekvenssitallennuksessa sekvenssien määrän maksimointi näytenopeuden kustannuksella)
Mikäli käytät enintään kahta kanavaa ja oskilloskoopissa (Siglent X mallit) on 4 kanavaa valitse tällöin käytetävät kaksi kanavaa siten että käytössä on maksimi näytenopeus.

3. Jos tutkittavat signaalit ovat kanttiaalto tyyppisiä ja epäilet esimerkiksi nurkkien ylilyönnin olevan Sin(x)/x aiheuttama "Gibbs ears" ilmiö (Kuva 2), kokeile ensin näyttömuotoa "Dots". Kun halutaan käyttää näyttömuotoa "Vectors" kannattaa ainakin kokeilla Sin(x)/x sijasta lineaarista eli x interpolaatiota.

4. Alias ilmiöitä voi myös joissain tilanteissa vähentää kytkemällä 20MHz kaistaleveys käyttöön erityisesti silloin kun toimitaan 50MSa/s tai alemmilla näytetaajuuksilla jotta vähennetään AD muuntimelle pääseviä korkeita taajuuksia jotka aiheuttaisivat alias muodostusta. Lisäksi joskus saattaa tässä tarkoituksessa olla apua myös siitä että kytkee mittapään toimimaan 1x asetuksella joka rajoittaa myös korkeampia taajuuksia.

5. Jos näet hitaahkoilla pyyhkäissyajoilla ja matalilla näytenopeuksilla jonkun epämääräisen aaltomuodon joka ei halua triggautua. Esimerkkinä tilanne jossa sisään tulee tasan 10MHz siniä ja oskilloskoopin näytenopeus on esim 100kSa/s (1 kanava, muisti 14k, 10ms/div) saatat nähdä suuruusluokkaa yleensä alle 100Hz siniaallon tapaista. Itseasiassa sen taajuus on se ero joka sinun oskilloskoopin referenssi poikkeaa 10MHz sisääntulevasta taajuudesta eikä siihen pysty triggaamaan. Hätäisimmät on kysyneet että onko oskilloskooppi jotenkin sekaisin tai onko siinä vikaa...  Ei ole vikaa. Se toimii niinkuin teoria sanoo.
Muuta nyt muistiksi 14M. Näytenopeus on nyt 100MSa/s. Siirry zoomaukseen ja veivaa alaikkunaan näkyviin 20ns/div ja näet 10MHz siniä joka itseasiassa myös triggaa hyvin koska nousunopeus ei riko sääntöjä. Siirry takaisi pois ikkunoidusta zoomauksesta. Muistiksi 14k. taas näkyy se matalataajuinen ei triggaava sini.
Muuta nyt Acquisition Normal sijaan PeakDetect. Huomaat kuinka signaali on nyt yksi keltainen palkki vaakasuoraan jossa näkyy alkuperäisen 10MHz sinin peak-peak verho.
Eli yksi tapa lisää tarkistaa signaalia... vaihda peak detect toimintaan ja päättele tuloksesta.

6. Jos näet nopean kanttiaallon nurkkien "lepattavan" (nurkkien taso- ja aikajitteriä) niin silloinkin on syytä epäillä. Kokeile dots näyttömuotoa, maksimoi samplenopeus, kokeile Sinc sijasta linear vector näyttötavalla.

Kun hallitsee näitä eri keinoja ja tietää mistä on kyse silloin alias yms ilmiöt eivät johda harhapoluille lainkaan niin helposti. Analogisten oskilloskooppien kanssa koko tätä ilmiöjoukkoa ei ole.  Niissä ei voi syntyä lainkaan alias ilmiöitä eikä interpoloinnin tuottamia ilmiöitä - siksikin nämä voivat oudoksuttaa mikäli aiemmpi kokemus perustuu analogisiin oskilloskooppeihin.


Kohtaan 5. liittyen pari esimerkkiä.



Kuva 7.
Alkuperäinen signaali joka on käytössä kuvissa 8. sekä 9.  Signaalin taajuus 45MHz reunojen nopeus luokkaa 4ns.
Koska kuvassa on käytössä 1GSa/s näytenopeus luonnollisestikaan ei esiinny aliasointia. Sattumoisin kuvassa näyttötapana on Dots jolloin pelkät näytepisteet tulostetaan ruudulle ilman pisteitä yhdistäviä suoria tai Sinc interpolaation tuottamia viivoja. Koska oskilloskooppi on nopeahko DPO tyyppinen ehtii se tuottaa niin paljon pisteitä ruudulle että yksittäiset pisteet ei erotu juurikaan edes noilla jyrkemmillä reunoilla.




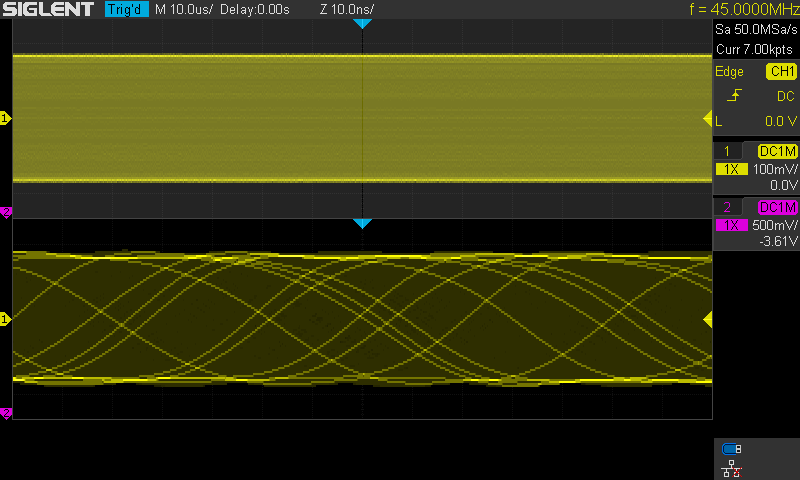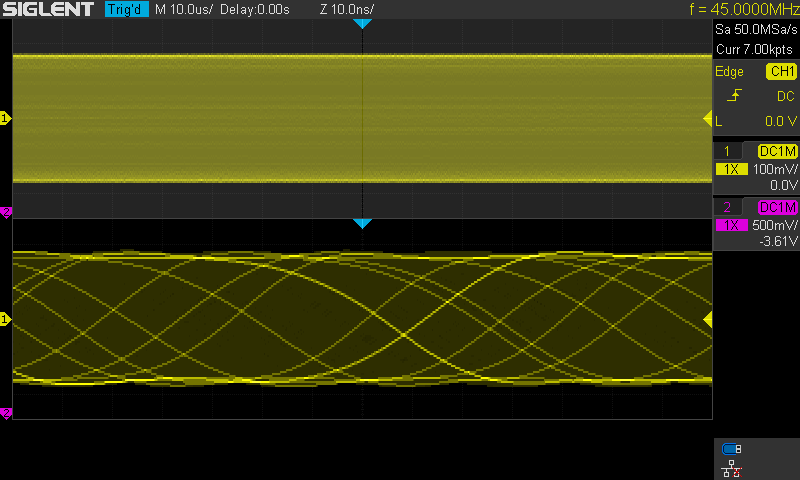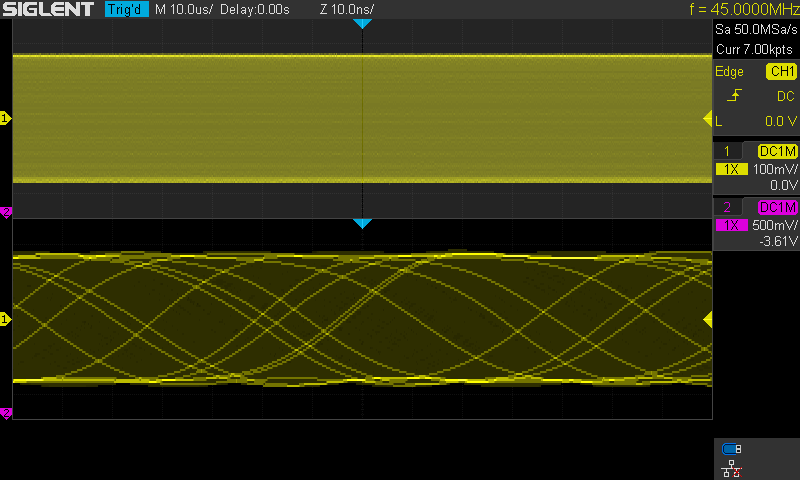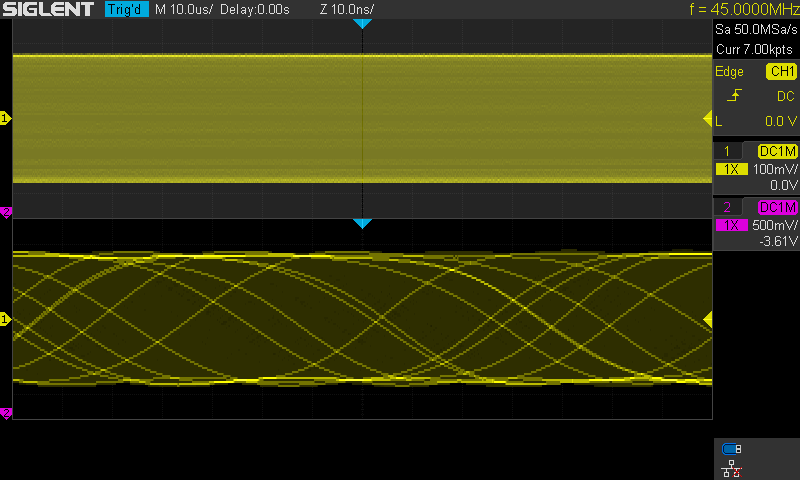
Kuva 8.
Signaali sama kuin kuvassa 7. Kuvan tapauksessa Sin(x)/x on käytössä. (ja luonnollisesti Vectors näyttömuotona)
Kuvassa on hidastettu vaakapyyhkäisyä ja rajoitettu vaakapyyhkäisyn muistin pituudeksi 7k.
Näin saatu näytenopeus pakotettua tätä demonstraatiota varten 50MSa/s nopeuteen. Tämä nopeus on ehdottomasti aivan liian alhainen kyseiselle signaalille. Näytteiden väli on 20ns. Signaalin nousuaika on luokkaa 4ns ja koko jakso hiukan yli 22ns. Kyseinen signaali vaatisi miellellään vähintään yli 500MSa/s.


Seuraava on varsin tärkeä ymmärtää ja muistaa myös soveltaa joissain käyttötilanteissa.
Se myös mukavasti osoittaa käytännössä sen että digitaalinen triggausjärjestelmä ei perustu siihen desimoituun dataan jota näemme silloin kun samplenopeudeksi ilmoitetaan jokin muu kuin AD muuntimen perusnopeus, jota se aina käyttää. Niitä nopeuksia on kaksi. Joko 1GSa/s tai 500MSa/s riippuen montako kanavaa on yhtaikaa käytössä. Tässä alla olevassa esimerkikssä AD muuntimen nopeus on 500MSa/s ja desimoitu nopeus 50MSa/s.  Triggausjärjestelmä käyttää tässä tapauksessa 500MSa/s dataa. Alla kuva 9. GIF animaatio näyttää suuntaa miltä tilanne suurin piirtein näyttää livenä ruudulla.


Kuva 9.


Näyttömuotona Kuvassa 9 on nyt pisteet (Dots) ja edelleenkin näytenopeus on alhainen. Katso myös ylempää kuva 4.
Nyt meillä näkyykin signaali aivan ok ja jopa triggaus toimii tarkasti (ja hienosäätää signaalin kohdalleen näytepisteiden väliin oikeaan kohtaan kullekin vaakapyyhkäisylle, miten se edes on mahdollista...  (no on siihen selitys mutta en pura sitä tähän tämän enempää: Muistutan vain että AD muuntimen nopeuttahan ei muuteta vaan datavirtaa on desimoitu jotta on saatu 50MSa/s vastaava näytejono jonka pisteet ovat toki näytöllä esitettävän Sinc interpoloinnin käyttämä data)

Jopa tälläkin asetukselle oskilloskooppi ehtii tuottamaan yhteen TFT frameen useita vaakapyyhkäisyjä jolloin silmä noiteeraa niitä enemmän kuin yksittäinen frame kuvattuna still kuvaksi (kuvassa noin 15 jokaiseen TFT frameen ja se nopeus taas on luokkaa 25frame/s). Jokaisessa vaakapyyhkäisyssa kuitenkin näytepisteet ovat satunnaisessa sijainnissa signaaliin nähden. (Tietenkin koska signaalin ja oskilloskoopin ADC kellon välillä ei ole lukitusta.)

Voidaan sanoa että oskilloskooppi toimii tavalla jolle voimme antaa nimen Sequential Acquisitions Random Interleaving  eli SARI. (jollain tavalla sukua LeCroyn "Random Interleaved Sampling mode" eli  RIS  toimintatavalle)
Tätä ei ole Siglentin toimesta missään erikseen mainittu tai selitetty mutta näin se kuitenkin toimii. Pitää kuitenkin huomata että tälläkin on rajansa. Kuten kuvassa nähdään signaalin triggaava taajuus on kuitenkin alle 2*fNyq eli alle näytenopeuden.  Miksi ominaisuutta ei ole dokumentoitu. Mahdollisesti siksi että nykyisellään sen määrittely spesifikaatioihin olisi hankalaa ja/tai mahdollisia sekaannuksia aiheuttavaa. Mutta, kuten olen aina sanonut, tunne laitteesi! Laitteen ominaisuuksia kannattaa ns itseopiskella.


Seuraavassa kuvassa, Kuva 10. on tilannetta hiukan purettu. Poimittu ylläolevasta yksi TFT frame. Ja lisäksi siitä framesta merkattu yksi yksittänen vaakapyyhkäisy tai capture tai acquisition kuinka sitä sitten nimittelemmakin.


Kuva 10.

Kuvassa 10 on Kuvan 9 gif animaatiosta yksi frame.
1 frame tässä on sama kuin olisi otettu oskilloskoopin käydessä yksi TFT ruutu. Koska oskilloskooppi on DPO tyyppinen yksi frame voi sisältää useita vaakapyyhkäisyjä. Kuvamuotona on nyt pelkät datapisrteet. Kuvassa on ehtinyt tapahtua 16 vaakapyyhkäisyä jossa kukin sisältää 7 datapistettä. Olen merkinnyt yhden yksittäisen trigatun vaakapyyhkäisyn pisteet pinaisella ympyrällä. Datapisteiden ajallinen väli on 20ns koska meillä on nyt samplenopeus 50MSa/s. Kuitenkin kuten nähdään ne 7 datapisteen pyyhkäisyt on trigattu ja asemoitu aivan kohdalleen. Sehän ei olisi mitenkään edes teoriassa mahdollista tässä tapauksessa mikäli triggaus perustuisi niihin datapisteisiin jotka on nöytöllä. Kuvassa on Persistence kytkettynä päälle joten näkee missä ne ovat olleet myös ajassa taaksepäin niin kauan kun Persistence on niitä siihen kumuloinut.
Kuvassa siis nähdään 16 pyyhkäisyä ja niiden kunkin 7 pistettä sekä edeltäviltä TFT frameilta tuo persistence jälki.
Kuten nähdään, triggaus ja on onnistunut kohtalaisenkin tarkasti. No onhan triggaus käyttänytkin pyyhkäisýn ajan datavirtaa jossa näyteväli on 2ns.

Tämä on käytännön esimerkki joka osoittaa sen että Triggausjärjestelmä saa ennen desimointia käyttöönsä desimoimattiman datan. Desimointi tapahtuu vasta triggauksen jälkeen (tai siis niin sen voi mielessään ajatella vaikka siellä sisällä jotain rinnakkainkin puuhasteltaisiin).
Tästä toki nyt sitten on myös seurauksia jotka joissain tilanteissa saattaa yllättää. Eli se että ruudulla olevassa datassa ei näykään syytä miksi on trigattu.
Ajattelepa tuota punakynällä merkittyä vaakapyyhkäisyä jos se vaikkapa olisikin ainoa vaakapyyhkäisy. Näkisit nuo punaisella merkatut ja ihmettelisit miksi on trigattu aivan hullussa kohdassa.

Ja nyt tarkkana.
Miten me oleme kuvassa käytäneet skooppia. Kaivetaanpas taas herrat Nyquist ja Shannon esiin. Olemme napanneet signaalia jonka perustaajuus on 45MHz eikä se ole edes siniä vaan hiukan kantin tapaista. Samplenopeus 50MSa/s. fNyquist on... kappas vaan 25MHz. Mites me tuolla lailla kuitenkin näemme signaalia.

Koska meillä triggaus toimii paljon suuremmalla nopeudella saamme nuo pisteet asemoitua (punaiset) mutta signaalista emme näe kuvaa tuon yhden perusteella... sitten tulee seuraava vaakapyyhkäisy. Taaskin joukko datapisteitä siitä signaalista ja triggaus osaa asemoida sen triggauskohdan... mutta pisteet ovat satunnaisessa sijainnissa triggauskohtaan nähden... sama seuraavalla kierroksella jne. Sattumalta pisteitä saadaan signaalin eri osista peräkkäisin pyyhkäisyin ja se alkaakin muodostaa kuvan signaalista.

Tämä toimii hiukan eri tavoin kuin ns ETS joissain oskilloskkoopeissa (aika harvinainen nykyisissa ns real time oskillokoopeissa) mutta tulos on osittain samankalatainen. Tämä EI toimi myöskään single shot tilanteissa. Signaalin pitää olla ns jatkuva signaali riittävän kauan jotta se signaalikuva aletaan saada.
Tässä aika hyvä tulos tuli jo noin 16 TFT framen aikana joissa  kussakin oli noin 16 vaakapyyhkäisyä joissa kussakin oli noin 7 datapistettä ja persistence vielä paransi asiaa. Toki ilman persistence olisi meillä verkkokalvolla aivan hyvä kuva signaalista jo tuollakin. TFT päivittyy noin 40ms välein joten sekunnissa noin 25 framea joissa näillä asetuksilla 16 vaakapyyhkäisyä eli wfm. Tässä tapauksessa nopeus on siis noin 400wfm/s. (16x25)

Muista siis että desimoiduilla näytenopeuksilla Trigger saa kuitenkin desimoimatonta dataa AD muuntimelta.
Muista että dots näyttämoodi on myös oikeasti hyödyllinen!
Tässä voitiin katsella signaalia joka oli 1,8 x fNyquist perustaajuutensa osalta ja se sisälsi ainakin yli 5 x fNyquist taajuuksia (kantin 3. Harmoninen on 5,4 x fNyquist).



Täydennän jossain vaiheessa lisää kun silmät ja aika sekä saatavilla olevat laitteet sallivat

--»  Ylös 

--»  Oskilloskoopit

--»  Etusivulle - Home