 FFT analysaattori, SDS2000X Plus.
FFT analysaattori, SDS2000X Plus. FFT analysaattori, SDS2000X Plus.
FFT analysaattori, SDS2000X Plus.
Kaikissa Siglent valmistamissa oskilloskoopeissa on FFT-analysaattori toiminto.
FFT ominaisuudet ja suorituskyky ovat eri malleissa
erilaiset.
SDS2000X Plus malleissa, FFT
ominaisuudet ovat varsin kehittyneet.
FFT maksimi pituus on 2M. Samanaikaisesti voidaan ajaa kahta FFT analyysiä
joiden kummankin pituus voi olla 2M.
FFT pituus on valittavissa välillä 1k - 2M (1k, 2k, 4k, 8k, 16k, 32k, 64k, 128k,
256k, 512k, 1M ja 2M)
Samaan aikaan voi olla käytössä enintään kaksi FFT (molemmat voivat käsitellä
joko saman kanavan signaalia tai eri kanavien signaaleja ja kummallakin on omat asetuksensa.
Kuitenkin siten että oskilloskoopin
samplenopeus on aina sama kaikille kanaville samoin kuin
oskilloskoopin näytemuistin pituus. Ne näkyvät kuvassa
päällekkäin kuten oskilloskooppikuvassakin eri kanavien signaalit)
Näyttö voi olla jaettu, "Split", siten että ylemmässä osassa näkyy
oskilloskooppikuvaa ja alemmassa osassa FTT tai siten että on koko näyttö, "Full
Screen", jossa kaikki on päällekkäin tai "Exclusive", näyttö jossa on koko
näytöllä ainoastaan FFT (yksi tai kaksi FFT).
FFT toimintamuoto "FFT Mode" voi olla "Normal", "Max-Hold" tai "Average".
Esim jos haluaa jokun taajusvastekäyrän voi käyttää Max-Hold yhdessä muiden
sopivien asetusten kanssa.
FFT "ikkunoita" on käytettävissä Rectangle, Blackman, Hanning, Hamming ja
Flattop joista viimeksimainittu on erityisen tärkeä silloin kun mitataan tasoja.
Alustukseksi yksi pieni esimerkki siitä mitä sillä muun muassa voi
tehdä.
Seuraavat kaksi kuvaa on yksi ja sama tilanne. Olen vain valinnut ensin F2 ja
seuraavassa kuvasaa F1 joloin asteikko vaihtuu sen mukaan kumpi on viimeksi
valittu.
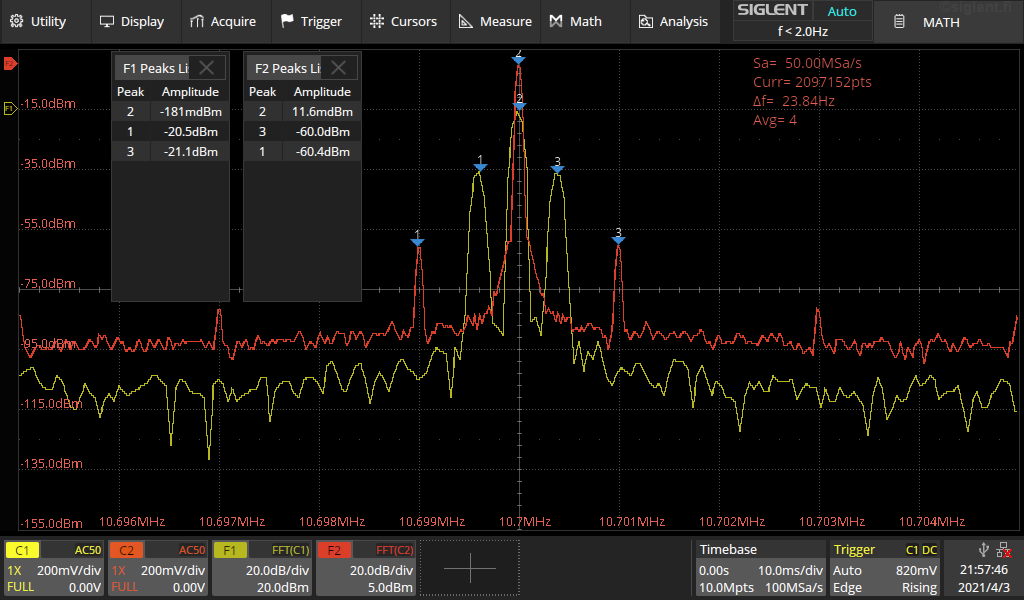
Kuva 1a.
Kuvassa FFT (F2) 10,7MHz AM signaali 1kHz modulaatiolla ja 0,2%
modulaatiosyvyydellä. Tällöin sivunauhat -60dBc.
Samassa kuvassa toinen FFT (F1) jossa 455kHz AM 200Hz modulaatiolla ja 20%
modulaatiosyvyydellä jolloin sivunauhojen taso -20dBc
Huomaa että kuvissa 1a ja 1b on koko ajan näytöllä sama tilanne, ainostaan olen
vaihtanut asteikot klikkaamalla alapalkissa olevaa F2
Tokihan tuossa koko ajan samalla päivittyy kumpikin FFT eli mistään stop tilasta
ei suonkaan ole kyse.
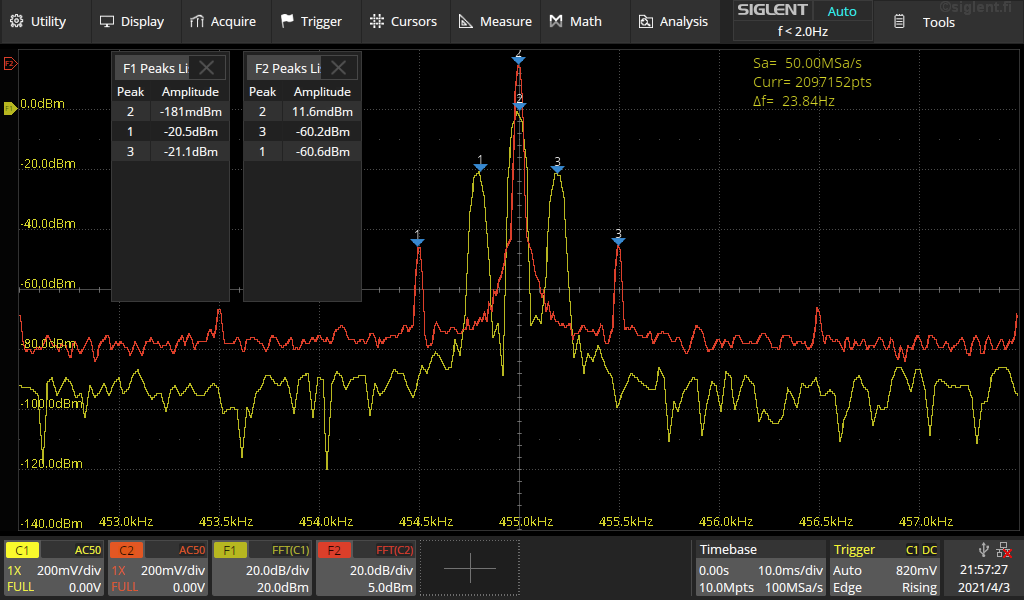
Kuva 1b.
Samassa kuvassa toinen FFT (F1) jossa 455kHz AM 200Hz modulaatiolla ja 20%
modulaatiosyvyydellä jolloin sivunauhojen taso -20dBc
Kuvassa FFT (F2) 10,7MHz AM signaali 1kHz modulaatiolla ja 0,2%
modulaatiosyvyydellä. Tällöin sivunauhat -60dBc.
Kuvissa 1a ja 1b on koko ajan näytöllä sama tilanne, ainostaan olen
vaihtanut asteikot klikkaamalla alapalkissa olevaa F1
Koko ajan samalla päivittyy kumpikin FFT eli mistään stop tilasta
ei suonkaan ole kyse.
Luonnollisesti useinmiten katselemme vain yhtä FFT. Nuo kuvat ovat vain
esimerkkinä että kahta FFT voi yhtaikaa katsella. Kumpikin FFT voi olla eri
kanavalta tai samalta kanavalta esimerkiksi eri taajuudelta ja erilaisin näyttö
ym parametrein.
Huomaa että SDS2000X Plus mallissa voi olla matematiikka funktioita samaan
aikaan enintään kaksi joten muita matematiikka funtioita ei voi olla käytössä, FFT kuuluu
matematiikkafunktioihin.
Hiukan perus FFT asioihin liittyviä ilmiöitä.
Olennaisia seikkoja ovat näytenopeus sekä FFT pituus. Ne määräävät
taajusresoluution ja taajuusrajat.
FFT alkaa aina taajuudesta 0Hz.
FFT päättyy aina taajuuteen sampletaajuus/2. Ja tässä sampletaajuus on nimenomaan
FFT sampletaajuus. Oskilloskooppi (time domain) sattaa silti käyttää toista
isompaa samplenopeutta.
FFT Δf = FFT sampletaajuus/FFT samples. Esimerkki:
FFT samplenopeus 2GSa/s (taajuus siis 2GHz) ja pituus 1048576 pts. (1M FFT)
2000000000Hz/1048576=1907,348633Hz. Näytteiden taajuusväli eli Δf joka näytöllä
näkyy Δf= 1,91kHz
Flattop RBW (3dB) on noin 7,11
kHz. noin 3.72 x Δf (jos mittaa sen kursoreilla FFT näytöltä pitää huomata
että näytöllä on lineaarinen interpolaatio FFT pisteiden välillä jotan sieltä
saa hiukan liian kapean arvon)
Ikkunoiden ominaisuuksissa on tietysti muitakin eroja kuin vain pääkeilan -3dB
kaistaleveys.
FFT käyttämä samplenopeus näytetään FFT näytön
oikeassa yläosassa, samoin käytössä olevan näytemäärä sekä taajuusresoluution
Δf.
Flat top ikkuna on ainoa joka kunnolla soveltuu tasomittauksiin. Nimittäin FFT
jutuissa pitää muistaa nuo FFT näytepisteiden taajuudet. Esimmäinen on nollassa.
Siitä edetään Δf askelin! eikä näytteiden välissä mitään ole tietenkään. Nyt jos
ikkunan yläpää on kapea ja tutkittava taajuus osuukin johonkin noiden Δf
askelten väliin saadaan liian alhainen lukema. Flat top ikkunalla tuon seikan
aiheuttama tasovirhe on enintään noin 0.02dB. Kun se pahimmalla eli "Rectangle"
ikkunalla voi olla jopa likipitäen 4 dB. Selvennän asiaa kuvin jäljempänä.
Joskus näkee hiukan harhaanjohtavasti Δf sijasta nimitystä RBW. Mikäli näin on,
sillä ei ole tekoa sen RBW kanssa johon olemme tottuneet esimerkiksi
spetrianalysaattoreissa.
Mielestäni selkeämpää olisi että mikäli halutaan ilmoittaa RBW niin sitten
ilmoitetaan ikkunan pääkeilan (main lobe) 3dB kaistaleveys.
Erityisen suurta huomiota pitää kiinnittää alias ilmiöön silloin kun käytetään
FFT analyysiä. Jos meillä on 100MHz oskilloskooppi pääsee sisääntulosta AD
muuntimelle varsin korkeita taajuuksia. Mikäli esimerkiksi 200MHz olisi 10dB
vaimentunut se ei ole paljon kun katsellaan FFT signaalitasoja logaritmisella dB
asteikolla.
Mikäli AD muunnin toimii 2GSa/s ei siellä synny varsinaista aliasointia kuin
vasta 1GHz rajan yläpuolella. Tämä ei olekaan silloin se isompi ongelma. Huomaa
kuitenkin että FFT näytenopeus voi olla paljonkin alempi kuin oskilloskoopin AD
muuntimen ja oskilloskoopin käyttämä täysi tai desimnoitu näytenopeus. FFT
näytenopeus voi olla niitä alempi.
Usein haluamme katsoa FFT jollain paljon alemmalla taajuuskaistalla
kuin 0 - 1GHz! Samoin usein haluamme kohtalaisen hyvää resoluutiota. Se
miten asetamme FFT asetukset on monen tekijän kompromissi, joista tärkeää on sen
taajuusalue, taajuusresoluutio ja FFT päivitysnopeus. Niistä myöhemmin.
Ajatellaan että FFT pituus olisi 100ksample, FFT samplenopeus 1MSa/s
(1000000Hz). Taajuusalue (full span) olisi tällöin 1MHz/2 eli 0 - 500kHz. "Resoluutio" Δf olisi 10Hz
( 1000000Hz / 100000 = 10Hz).
Resoluutio ei tarkoita että voit erottaa kaksi signaalia toisistaan jotka ovat
tuon Δf etäisyydellä toisistaan. Käytännössä Blackman ikkunalla noin 4xΔf
alkaa erotta signaalit kun niiden taso on lähes sama. Mutta johonkin 60dBc
tasolle saakka erottuvat toisistaan kun noin 9xΔf väli, Flat top ikkunalla
luokkaa 12xΔf .
Alempana lisää asiaa noiden FFT "ikkunoiden" (Hamming, Hanning, Blackman, Flat
Top ja Rectangle) ominaisuuksista.
FFT alias asiaa.
Tämä on pakollista ymmärtää ainakin jossain määrin. Muussa tapauskessa FFT
käyttö on vain "ihmeellisten ilmiöiden viihdekatselua"
Otan esimerkiksi tässä tilanteen jossa FFT näytetaajuus on 1MHz (1MSa/s)
Olemme asetelleen näytön siten että vasemmassa reunassa on 0Hz ja oikeassa
reunassa 500kHz joka on tässä tapauksessa kyseisen FFT full span.
Mikäli meillä tulisi sisään yksi puhdas 490kHz
siniaalto ja oskilloskoopinkin kaikki tuloasteet ideaalit ja näytteitys olisi täydellistä
näkisimme yhden signaalipiikin taajudella 490kHz.
Alias ilmiö ei tässä esiinny nyt lainkaan.
Alias.
Ajatellaanpa että jostain syystä muuttaisimme signaaalimme taajuudeksi
510kHz. Mitä nyt näkisimme... sehän meni yli laidan eli katosi näkymättömiin,
eikö niin.
Ei, tämä ei mene
lainkaan niin...
Näkisimme tasan tarkkaan 490kHz signaalin aivan kuten silloinkin kun sen
signaalin taajuus oli 490kHz. Tämä nyt näkyvä signaali sensijaan onkin nyt 510kHz
signaalin alias.
Mikäli syättäisimme korekemman taajuuden, sanotaan vaikkapa 600kHz. Meidän
näkyvä taajuuspiikki siirtyisi alemmas. Näkisimme 400kHz signaalin FFT näytöllä.
Nostetaampa taajuutta edelleen lisää. Syötetään sisään 1450kHz. Nyt näkisimme
FFT näytöllä 450kHz ja kun nostetaan edelleen sanotaan vaikka 1550
taajuudelle... mitä ihmettä edelleen näkyy 450kHz. Mitäs tämä nyt on...
Eli miksi usen näemme niin sekavaa "hässäkkää" FFT näytöllä.... varsinkin
silloin kun signaali sisältää harmonisia ja mahdollisia epäharmonisia.
Ajatellaanpa lisää.
Otetaan mukaan käytäntö. Ajatellaan että tuolla 490kHz signaalilla on sen
perustaajuuden lisäksi, joka siis on 1. harmoninen, myös harmoniset 2. ja 3.
Eli FFT näkee nyt taajuudet 490kHz, 980kHz sekä 1470kHz. Sovitaan että niiden
tasot ovat 1. 0dBm, 2. -40dBm ja 3. -20dBm.
Mitäpä mahtaisi näkyä näytöllä olettaen että koko taajuusalueella, mukaanlukien
nuo harmoniset, on skoopillamme tasainen taajuusvaste.
Näkyisi perustaajuutemme eli 1. harmoninen 490kHz taso 0dBm tietenkin. Sitten
2. harmoninen taajuudella 20kHz -40dBm ja
3. harmoninen taajuudella 470kHz -20dBm.
Nyt kun katsoisit sellaista kuvaa jossa taajuuspiikit 20kHz, 470kHz ja 490kHz
tiedätkö että ne kaksi ovat tuon perustaajuuden harmonisia. Ei se niistä
mitenkään näy. Ei ne vilkuta sinulle että hei mä olen harmooni...
Entä mitä mahtaisi näkyä jos meillä olisikin perustaajuutena 250kHz sinin
näköistä ja sillä kaikki
harmoniset aina 7. saakka ja sellaisella tasolla että ovat paljon
yli kohinatason.
Näkyisi yksi 250kHz signaalipiikki. Harmoniset ovat 2. 500, 3. 750, 4. 1000, 5.
1250, 6. 1500 ja 7. 1750kHz. No, hetken kun miettii niin asiahan on selvä, osa
harmonisista osuu nollaan ja osaa ylärajaan ja osa samaan missä on meidän 1.
harmoninen eli perustaajuus johon kohtaan osuu 3. ja 5. sekä 7. Nollataajuuteen
osuu 4. ja ylärajaan 2. ja 6.
Miten tuo "toimii". Juuri tämä FFT alias juttu, folded back taajuuksien
juttu tulee ymmärtää, muuten näet lähinnä "ihmeellisiä ilmiöitä".
Lankaleikki ("folded back" periaate):
Ajattele että taajuus, esimerkiksi 1600kHz on 1600 pitkä lanka. Taajuusalue on 0
- 500 ja sen molemmissa päissä on seinät jossa on koukkuja lankaa varten.
Kiinnitä lanka seinään 0 ja lähde matkaan kohti seinää joka on matkan 500
etäisyydellä. Koska 1600 pituinen
lanka ei lopu ennen seinää 500, laita se koukkuun ja käänny kohti 0 seinää (1.
fold back),
sinulla on vielä 1100 pituinen pätkä. Saavut seinälle 0. Kiinnitä lanka seinän 0
koukkuun, sinulla on vielä lankaa jäljellä 600 ja jatka taas matkaa (2. fold
back) kohti seinää
500. Seinälle 500 saapuessasi lanka on vielä jäljellä 100, palaa kohti seinää 0
(3. fold back).
Lanka loppuu kun olet seinien välisessä kohdassa 400. Siihden piirretään sitä
sitä signaalia vastaava merkki.
Siis, kun FFT näytenopeus on 1 Msa/s (näytetaajuus 1MHz) meillä on taajuusalue 0
- 500kHz. Kun signaali on 1600kHz se ei katoa mihinkään ulkopuolelle vaan näkyy
taajuudella 400kHz.
Tässä on hyvä huomata että parittomat "fold
back" taajuudet näytetään peilikuvana eli jos oli esim AM modulaatio niin nyt
sivunauhat vaihtavat paikkaa! Jos siis taajuus on 0 _ 1fNyquist
signaali on normaali ja oikein päin. 1fNyquist _ 2fNyquist se on peilikuva, seuraava eli 2fNyquist
_ 3fNyquist väli näkyy taas oikein päin.. 3fNyquist
_ 4fNyquist näkyy taas peilikuvana.... jne.
Aivan sama jos tarkastelet signaalia joka on parittomalla fold back jaksolla
näkyvissä ja nostat sen taajuutta se liikku kuvassa alempaan taajuuteen päin.
Tuota kannattaa kokeilla FFT ja generaattorin kanssa muutamiakin kertoja jotta
se tulee aivan selväksi.
Kaikki signaalit, on ne sitten kanttia tai sahalaitaa tai mitä tahansa
vaikka vapaita
aaltomuotoja ne voidaan loppujen lopuksi esittää joukkona eri taajuisia (ja tasoisia ja
vaiheisia) siniaaltoja. Ota nyt tutkittavan signaalin jokaista sellaista taajuskomponenttia vastaava
langan pätkä ja aseta niiden alku nollaan. Lähde niiden kanssa matkaan... jos
mikään niistä ei ylitä pituutta 500 tässä tapauksessa ei synny mitään aliaksia.
Jos yksi tai useampi on pidempi, niin niiden kanssa sitten niin kauan kuin
kussakin pituutta (eli taajuutta) riittää. Nyt varmaan huomaat että näytölle
syntyy melkoinen kaaos.
Mistäs nyt tiedät mikä niistä taajuspiikeistä on
alias ja mikä taajuusalueella. Yksinkertaisesti. Et mistään, ellei signaalista
ole mitään muuta tietoa kuin saatu yksi FFT näyttö.
Miten selviytyä näiden kanssa tai ainakin tunnistaa aliakset.
1.
Varmin keino on viedä se ylempi "kääntöpiste" (FFT maksimi taajuus eli FFT
näytetaajuus/2 ) niin ylös
ettei mikään sisään menevista taajuuksista ylety sinne saakka. Tällöin aliakset katoaa.
(huomaa että myös oskilloskooppi voi generoida harmonisia kun esim signaali
leikkaa)
2. Toinen on tietenkin se että otetaan pois ne taajuudet jotka
olivat liian korkeita. Silloinhan ei ongelmaa synny. Alipäästösuodin.
3. Jos voimme muuttaa tutkittavaa signaalia voi kokeilla hiukan nostaa tai
laskea taajuutta. Silloin helposti näkee kuinka ne taajuuspiikit kulkevat,
päinvastaiseen suuntaan kulkevat ovat ainakin aliaksia.
4. Muunlainen tunnistaminen. Esimerkiksi jos signaali on kantin tapaista jossa
on runsasti harmonisia jotka alenevat tasoltaan mitä ylemmäs sarjassa mennään.
Kun näet silloin FFT näytön oikeasta reunasta koti nollaa jonon signaaleita
joilla on aleneva taso on aika helppo olettaa että ne ovat niitä taaksepäin
kohti nollaa taitettuja harmonisten aliaksia. Ne voi jatkua jopa niin pitkään
että taittuvat vielä takaisinkin sieltä vasemmasta reunasta.
Keinoja siis on.
1.
Nostetaan FFT näytetaajuus niin että ylärajataajuus on ylempänä kuin korkeimmat
signaalissa esiintyvät taajuuskomponentit. Tämä on tietenkin hyvä keino,
hankaluutena vaan on käytännössä se että taajuusresoluutio putoaa ellei samassa
tahdissa nosteta FFT näytepituutta. Tätä voi usein kuitenkin käyttää aliasten
tunnistamiseen ja sitten palata alemmalla näytetaajuudelle kun
tietää ne aliakset.
2.
Asetetaan signaalitielle alipäästösuodatin joka estää yli FFT ylärajatajuuden
(fNyquist) olevat taajuuskomponentit.
Tätä myös käytetään kun tehdään hyvälaatuisia FFT analyysejä.
3. Jos voit, muuta hivenen tutkittavaa taajuutta ja tarkkaile signaalipiikkien
liikkumista, ainakin osa aliaksista paljastuu.
Tärkeintä on kuitenkin tietää tämä asia jotta voi jo tiedon avulla arvioida
näytön näkymää. Jos vielä voi tehdä muutaman kokeen signaalin kanssa saattaa
päästä paremmin perille siitä mikä näytöllä on mitäkin.
Joskus FFT asetusten tekeminen on varsin työlästä ennen kuin läytyy optimaaliset
asetukset. Siinä ei hoppuilu hyvää tee, ei ole ihan sellainen säädä vähän
kaikkea nopeasti sinne tänne. Se vaatii joskus kokeneeltakin aika paljon vaivan
näköä jos aikoo saada aikaan jotain kohtalaisen kunnollista.
Alias ilmiö ei ole aina pelkästään huono asia. Sitä voi
joissain tilanteissa käyttää hyödyksikin.
Alinäytteitys! Undersampling!
Aina ei ehkä tule ajatelleeksi sitä puolta asiassa. On aika
jännää että tästä puhutaan suht vähän. Aina vaan kauhistellaan aliaksia kun
niitä voi osaavissa käsissä todellakin hyödyntää. Seuraavassa esimerkiksi
parantamaan resoluutiota.
Kun tuota ylärajaa, eli "Nyquist" taajuutta nostetaan törmätään siihen että
resoluutio alenee kun emme voi nostaa FFT näytepisteiden määrää. Joka esim
SDS2000X Plus tapauksessa on 2Mpts, tarkemmin 2097152pts . Kun fsa on
näytetaajuus ja pts on yhden FFT näytejonon pituus, tällöin Δf = fsa/pts
Jos meillä on kiinteä FFT näytepituus ja taajuusaluetta nostetaan, joka siis
tapahtuu näytenopeutta nostamalla, taajuusresoluutio laskee koska
näytetaajuus/muistin pituus kertoo taajuus resoluution.
Halutaan katsella signaalia jonka kantoaalto on 145,5MHz.
Otetaan vain esimerkin vuoksi käyttöön "museomodulaatio" AM. Pistetään
modulaatiotaajuudeksi puheviestiliikenteen ymmärretyksi tulemisen perinteinen
alarajataajuus joka on 300Hz tuntumilla kun puhutaan ei tonaalisista kielistä.
Jos nyt valitsemme alimman mahdollisen näytenopeuden jolla 145MHz signaali ei
aliasoi on se SDS2000X Plus tapauksessa 500MSa/s. Jolloin saadaan tajuusalueeksi
0-250MHz. (Hh1 ja 2, FFT 2M, skooppi 500us/div, 5Mpts, 1GSa/s.),
toki sieltä löytyy myös 400MSa/s mutta silloin FFT
pituus on pienempi ja resoluutio hiukan heikompi.
Ei tarvitse edes enempää kokeilla, tiedetään heti ettei ole mahdollisuutta
erottaa noita sivunauhoja kantoaallosta koska Δf on tällöin 238,4Hz (bin
väli). Tuollainen 3xΔf alkaisi juuri ja juuri erottua Hanning ja Hamming
(ja rectangle) ikkunalla kun oikein hyvin arvaa. Tietää ainakin että jotain on
karkeasti jossain seuraavan bin kohdalla. Silloinkin Blackman ja Flat top
vain leviää ja voi lähinnä kuvitella että siellä on muutakin kuin puhdas
kantoaalto.
No, mitäs nyt... tehdäänpä
taikoja...
Otetaan käyttöön undersampling eli alinäytteitys. Siis halutaan
nimenomaan että se aliasoi.
Kokeillaanpas FFT näytenopeutta 50MSa/s. FFT taajuusalueeksi tulee 0-25MHz
jolloin signaali 145.5MHz näkyy taajuudella 4,5MHz. Aika monta kertaa on taittunut...
itseasiassa 5 kertaa (katso edellinen lankaleikki). Nyt Δf on 23,8Hz
ja 300Hz moduaaltio sivunauhat näkyvät vallan mainiosti erillään kantoaallosta
jopa Flat top "filtterillä" eli ikkunalla.
Käytimme alinäytteitystä. (skooppi 10ms/div. 10Mpts/100Msa/s ja FFT
50MSa/s ja keskitaajuus 4,5MHz ja span 5kHz.)
Mennään vielä hiukan pidemmälle... eli lisää resoluutiota jotta saadaan lähellä
kantoaaltoa olevat sivunauhat tarkasteluun.
Seuraava kuva on siis nimenomaan nyt rankasti alinäytteitystä käyttäen!
Katsotaan siis aliasta eli nyt harmillinen alias onkin otettu
hyötykäyttöön.
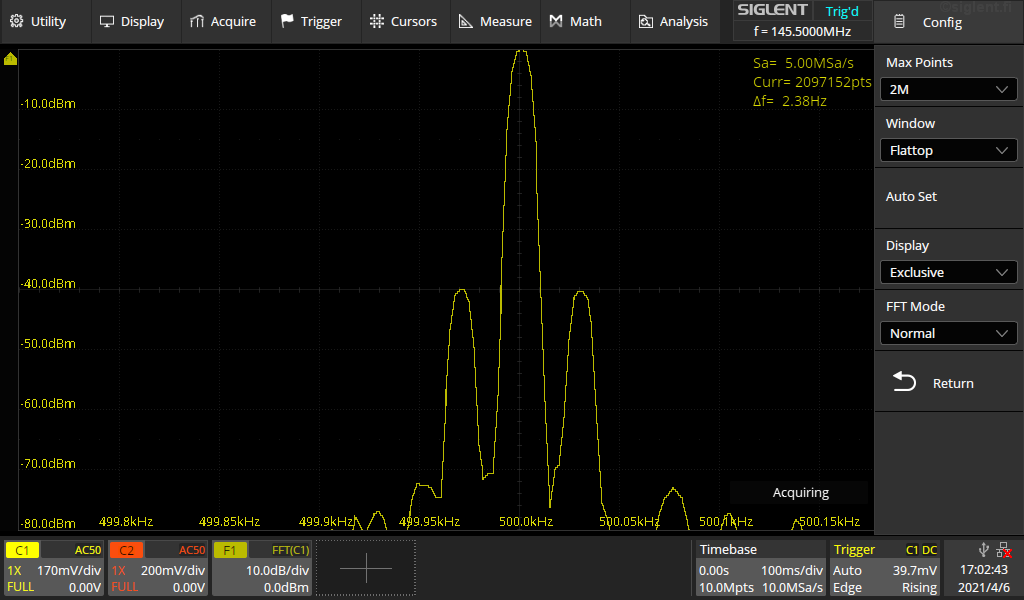
Kuva 3a.
Tässä halutaan siitä 145.5MHz signaalista erottaa 30Hz AM modulaatio (tai vaikka
50Hz hurina) joka lisäksi on melko matalalla syvyydellä, 2%.
Kuvassa on alennettu FFT näytenopeus 5MSa/s jolloin taajuusalue on 0 - 2,5MHz.
Tässä
tapauksessa signaalin 145,5MHz alias näkyy taajuudella 500kHz.
Kuvassa tuosta koko alueesta 0 - 2.5MHz on valittu näyttöalueeksi (Span) 500Hz
siivu. FFT ikkunaksi olen valinnut kaikkein leveimmän (ja tasotarkimman) Flat
top. Erottelukyky on nyt 30Hz
modulaatiolle sama kuin edellä 300Hz:lle. Nyt Δf on 2,38Hz. Kuvassa
modulaatiosyvyys on 2% jolloin sivunauhojen taso kuuluu olla -40dBc ja sehän
kuvassa näkyy. Kokeillin lisäksi että jopa 0,2% modulaatio, jossa sivunauhat on -60dBc tasolla, on eroteltavissa.
Toki aika rajoilla aletaan olla. 1% AM modulaatio ei jätä mitään epäselväksi
(-46dBc) ja vielä 0,5% modulaatilla sivunauhat edelleen vielä varsin
selkeät (-52dBc).
Kantoaallon tasonahan näissä signaaleissa on ollut 0dBm.
Erotimme siis oskilloskoopin FFT toiminnolla helposti noin 145MHz
kantoaallon vierestä 30Hz etäisyydellä olevat sivunauhat joiden taso on 40dB
kantoaallon alapuolella. Eikä erottelu tuota edes vaikeutta eli ei ole ns
rajatapaus. Ei tuota aivan äkikseltään uskoisi mahdolliseksi.
Eikä tässä edes kokeiltu äärirajoja. Toki ei tuo enää aivan nopeasti tapahdu.
Noin 3 sekunnin välein päivittyy tuo FFT.
Kuvassa taajuus 145,5MHz on välillä 58fNyquist_59fNyquist
joten signaali näkyy oikein päin (tuo ylempi on pariton).
145,5/2,5=58.2. Huomaa myös että kaikki muutkin signalait näkyisivät
tuossa kuvassa joten nyt pitää tietää se että meillä on vain signaali joka osuu
tuohon FFT ikkunaan taajuusvälillä 145MHz - 147.5MHz. Jos meillä on vain tuolla
taajuuvälillä olevie signaaleita silloin vain ne ovat tuossa FFT ikkunassa.
Mutta, jos meillä on myös joku muu signaali, esimerkiksi 500kHz se näkyisi
samassa kohdassa koska meidän FFT ikkuna on toidellisuudessa välillä 0 - 2,5MHz.
Jos meillä olisi koko tuo 2,5MHz ikkuna näkyvillä eli full span sen osalta,
näkisimme siinä kaikki signaalit jotka mahtuvat oskilloskoopin taajuusalueelle
väli 0-2.5MHz todellisena suoraan ja kaikki loput aliaksina siinä samassa
ikkunassa siellä mihin niiden
aliakset osuu siinä. Pitää siis tietää mitä tekee ja olla tarkkana.
Käyttäessä alinäytteitystä voidaan tietenkin rajoittaa muita signaaleja
häiritsemästä käyttämällä suodattimia, ali- yli- tai kaistanpäästö suodattimia.
Mikäli olisi käyttänyt sitä tavanomaista tapaa, 500MSa/s (0 - 250MHz FFT
taajuusalue) silloin ei olisi mitään mahdollisuutta erottaa noita sivunauhoja
kuten aiemmin jo totesin. Toki 3kHz modulaatio näkyisi silloin samalla tavalla
kuin 30Hz kuvassa 3.
Jos ajatellaan tuon Flat top ikkunan leveyttä niin siinä -3dB leveys on
suunnilleen 3xΔf.
UUsein tavallisten spektrianalysaattoreiden se erotuskyky jolla kaksi saman
tasoista signaalia voidaan erottaa on se taajuusero jolla muodostuvaan kuvaan
syntyy 3dB dippi niiden väliin. Kokeellisesti se on Flat top ikkunalla
suurinpiirtein 5xΔf. Toki riippuu mihin kohtaaan tarkalleen taajuus osuu. Kun
kokeilin 10 FFT keskiarvolla tuo oli kokolailla 5xΔf. Toisin sanoen tuolla
500MSa/s ja 2M FFT pituudella kaksi saman korkuista signaalia on erotettavissa
kun niiden väli on noin 1190Hz ja "filtterinä" tuo Flat top.
Kun toimitaan riittävän hyvin tunnetuilla
signaaleilla ja tutkittavan signaalin/signaalien
alias/aliakset pysyy FFT taajuusalueen ikkunan sisällä eikä muita
signaaleita/taajuuskomponentteja ole haittaamassa voidaan alinäytteityksellä tutkia
signaalia.
Mikäli siis törmäät siihen että taajuusresoluutio ei FFT:ssä riitä kun
työskentelet isommilla taajuuksilla. Älä heti heitä kirvestä kaivoon vaan mieti
edes hetki voisiko tätä alinäytteitys tekniikkaa mahdollisesti hyödyntää, vaikka useimmin
pyrimmekin nimenomaan välttämään signaalin aliasointia.
Lisäys 3/2024
Tässä on muutamia yleisesti
tunnettuja arvoja FFT ikkunoille. ( FFT_tutorial_NI.pdf )
Sitten tässä alla Keysight ilmoittamia tietoja.
Olen toisen mallisella Siglent oskilloskoopilla mitannut Siglentin Rectangular
(Uniform) Ikkunan -3dB RBW ja todennut että juuri kuten allaolevassa
"paperissa".
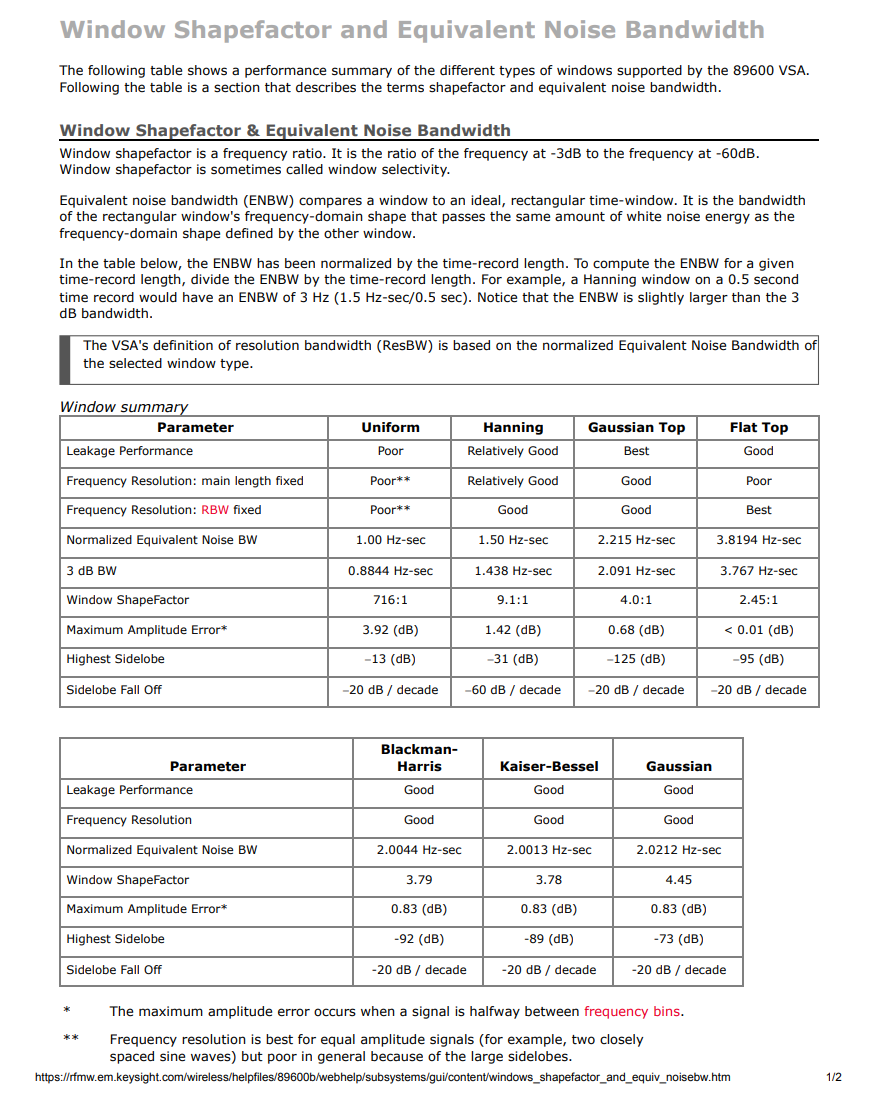
Tässä vielä toinen "paperi" samasta aiheesta.
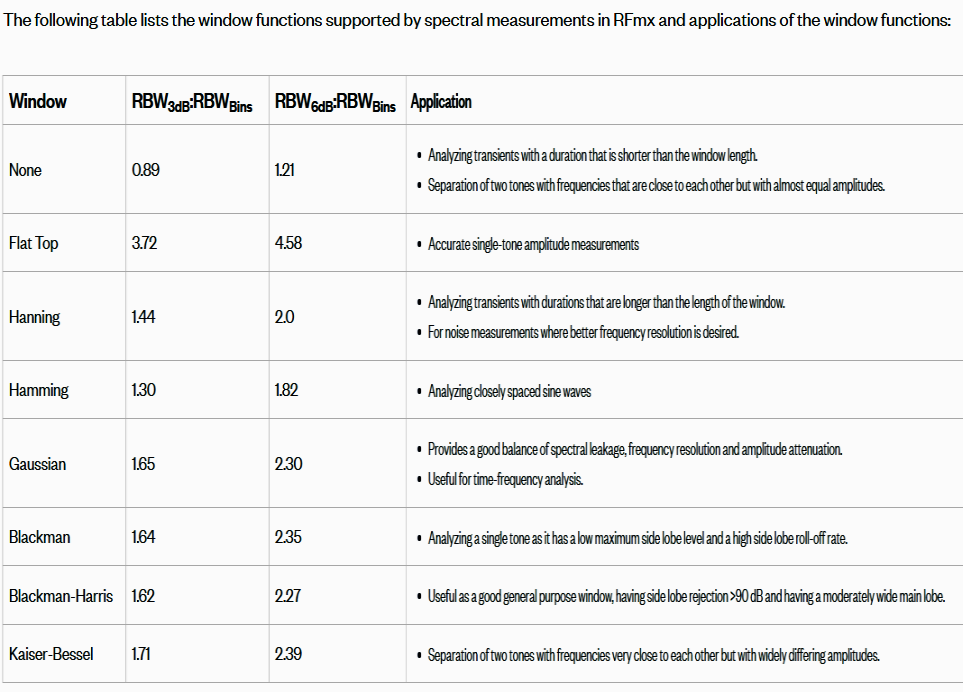
Siglentin FFT ikkunassa ilmoittamat RBW ovat kohtalasen hyvin linjassa näiden
kanssa (RBW3dB). (paitsi Rectangular (None, Boxcar, Uniform - rakkaalla lapsella
monta nimeä)
Tässä mitattu Siglentin SDS800X HD mallilla (aivan vain esimerkin vuoksi)
Rectangular ikkunan -3dB RBW.
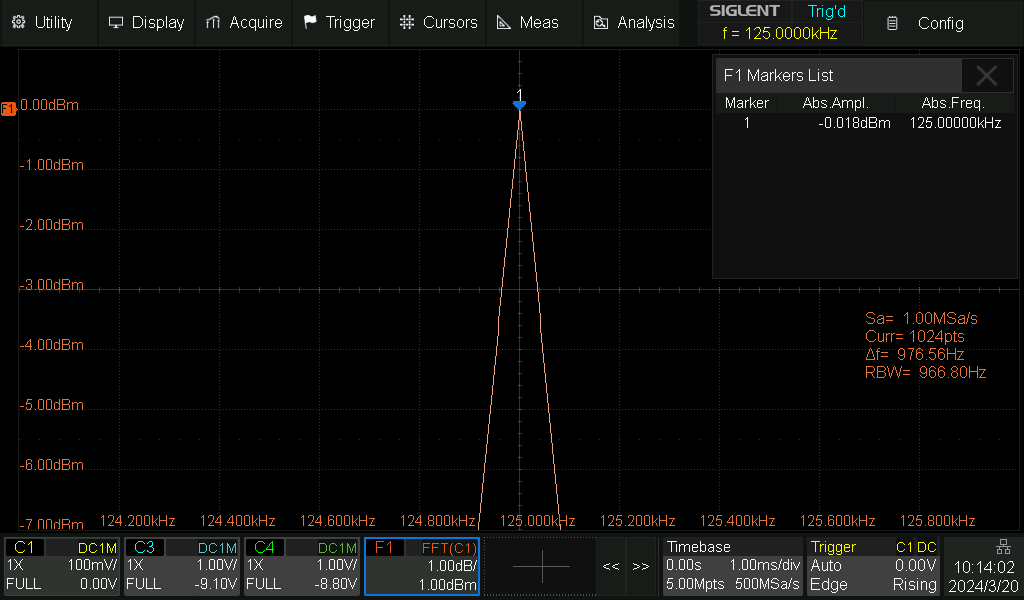
Ensin 0dB referenssiksi. (Huom tason mittauksen resoluutio ei riitä tuon
lähemmäs. Seuraava arvo olisi 0.02dBm.)
Tässä siis signaali tulee täsmälleen Bin taajuudella. Se "sattuu" olemaan
täsmälleen 125kHz (yksi Bin väli eli Δf on tässä tapauksessa
1000000Hz/1024=976.5625Hz)
(128x976.5625Hz=125000Hz)
Olen lisäksi passannut generaattorin siten että sen taajuus vastaa
oskilloskoopin käsitystä. (oskilloskoopin referenssin toleranssi on
+/-25ppm)
Keysight paperissa on mainittu että Rectangular (Uniform) ikkunalla -3dB BW on
0.8844 x Bin väli eli Δf
976.5625Hz x 0.8844 = 863.671875Hz. Tuosta siis keskilinjasta puolet tuosta
kummallekin puolelle, siis ~431.836Hz
RBW -3dB siis olisi 863.7Hz
Mutta jos joku mittaisi sen nyt tuosta kuvasta niin siinähän se on luokkaa 75Hz
joka on täysin virheellinen.
Millään muulla ikkunalla toki virhe ei ole noin valtava mikäli sitä kuvasta
suoraan mittaa.
Tilanne kuten kuvassa yllä ja nostan sisääntulevaa taajuutta juuri tuon 431.8Hz
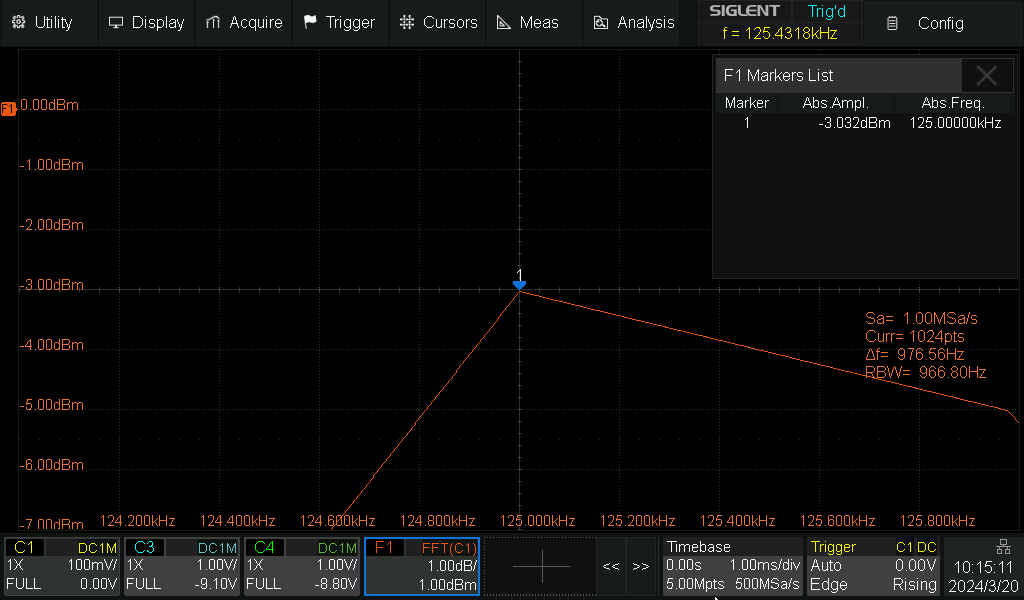
Kuten ylläolevasta kuvasta näkyy nyt taso on tippunut 3dB (taaskin tässä tulee
vastaan tuon taajuusmittauksen resoluutio)
Täsmällen samoin se putoaa (tuon horisontaalisena peilikuvana) jos pudottaa
taajuuden keskitaajuuden alapuolelle.
Voidaan siis todeta että ei ole ristiriitaa Keysight paperin eikä muidenkaan
kanssa.
Sensijaan tuo RBW jonka SDS800X HD esittää on hiukan outo. Joissakin lähteissä
toki mainitaan että ENBW olisi 0.99 x Δf ja siltä tuo mainittu arvo
näyttää.
Mutta ainakin "teoriakirjojen" mukaan kyseisen ikkunan ENBW (Equal Noise
BandWidth) olisi 1.0xΔf.
Tuossa kuvassa näytöllä on 2kHz (200Hz/div)
Korjaus 3/2024
Seuraavat allaolevat sisältävät osin virheellistä tietoa.
(Merkattu harmaalla taustalla: RBW asiat osittain väärin)
Suurin ongelma on se että FFT ikkunoilla ei ole tuollaista muotoa joka
kuvissakin ilmenee.
Kunkin Bin mittattu taso yhdistetään näytöllä suoraa viivaa käyttäen.
Mittaamalla tuolla tavalla RBW kiten alla on tehty johtaa enemmän tai vähemmän
vääräänn arvoon.
Ikkunan pääkeilan -3dB tason saa mitattua epäsuorasti mutta se on aika työläs
tapa.
FFT "ikkunat", moni kutsuu niitä filttereiksi kuten esimerkiksi
spektrianalysaattoreissa on RBW filtterit jotka ovat gauss tyyppisiä ja joilla
on jokin kaistaleveys. ilmoitettuna -3dBc tason leveytenä sekä lisäksi niillä on
jokin muotokerroin joka määrittyy useinmiten sen mukaan mikä on -3dB ja esim
-60dB leveyksien suhde.
FFTssä ei ole sillätavalla vastaavia filttereitä koska FFT kaikki perustuu
kulloiseenkin taajuusaskeleen Δf suuruuteen.
Alla olevat kuvat havainnollistavat niiden tarkempaa muotoa ja leveyttä.
Käytännössä emme koskaan katsele FFT kuvaa siten että ne olisi noin leveäksi
zoomattu. Kuitenkin nuo ominaisuudet on hyvä ymmärtää jotta ymmärtää
erottelykyvyn sekä mahdollisen tasovirheen joka johtuu siitä että tutkittava
taajuus ei osukaan juuri samoihin kohtiin kuin on Δf kerrannaiset alkaen
nollasta. Ainoa jossa niiden väli ei muodosta juurikaan tasovirhettä on Flattop.
Piirrä useita flattop ikkunoita vierekkäin niin että niiden keskietäisyys on Δf.
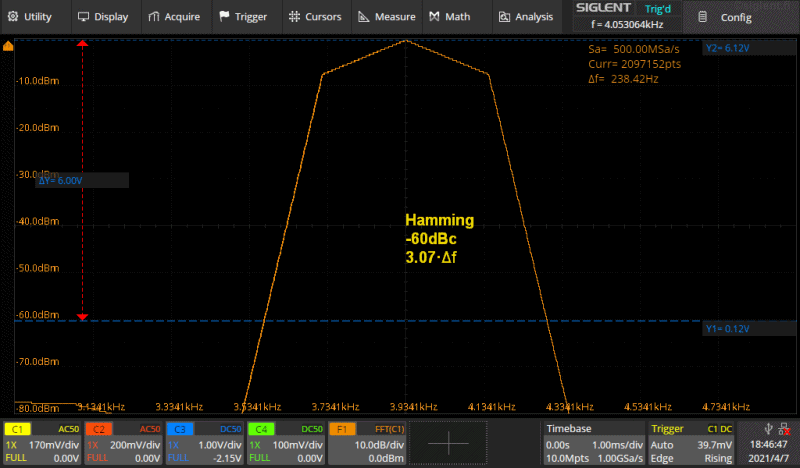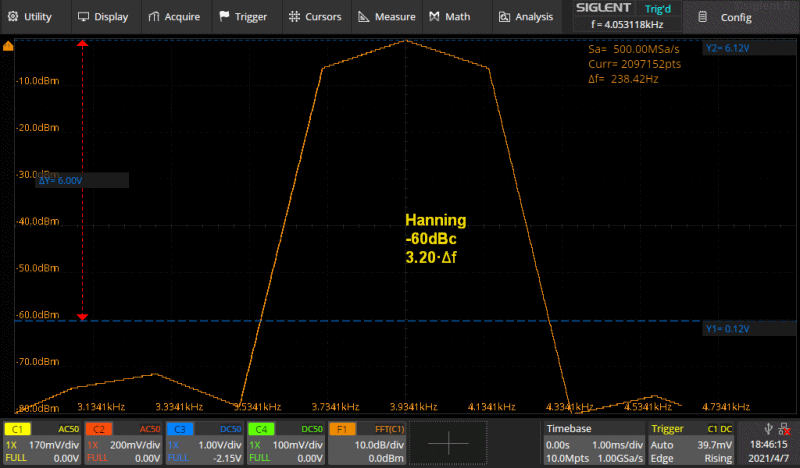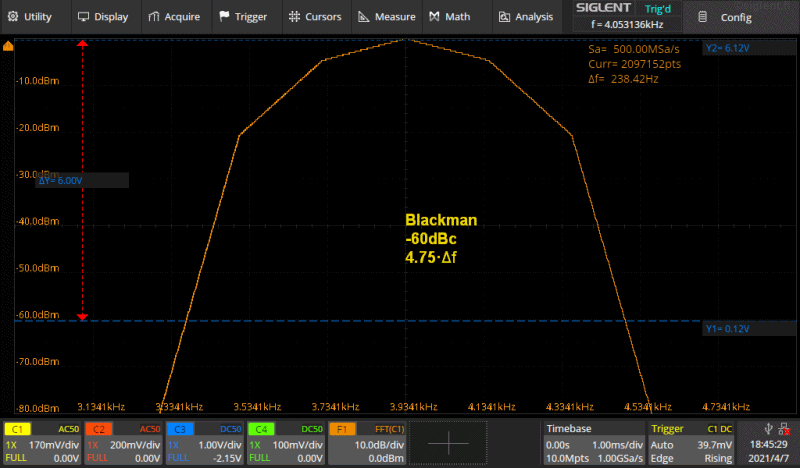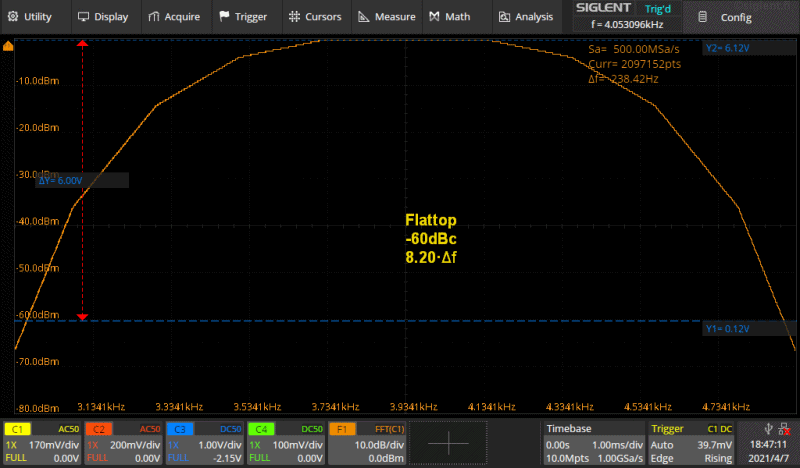
Kuva 5a. gif animaatio.
Kuvassa on Rectangle ikkunaa lukuunottamatta käytössä olevat ikkunat, Hamming,
Hanning, Blackman sekä Flattop peräkkäin. Asetukset on tarkoituksellisesti
asetettu siten että tuo muoto tulee kunnolla näkyviin. Oikeastaan tuo esitustapa
on hivenen valheellinen koska pisteiden väliin on piirretty suorat janat. Eihän
se tietenkään oikeasti niin ole, ei siellä mitään tuollaisia janoja, on vain ne
matematiikan tuloksena syntyneet pisteet. Niiden pisteiden väli taajuusakselilla
on juuri sen Δf suuruinen. Koska se resoluutio muuttuu asetuksista
riippuen muuttuu myös ikkunoiden leveys, siksi olen suuntaa antavasti laittanut
sille arvoksi n·Δf. Kuvassa siis suntaa antava leveys -60dBc
tasolla jolla tasolla on sininen kursori (älä välitä kursorin jännitearvoista,
sillä ei ole mitään merkitystä, ne katkoviivat ovat vain kuvassa selkeytämässä
asiaa).
Seuraavassa kuvassa aivan samat mutta vertikaali asteikko eri.
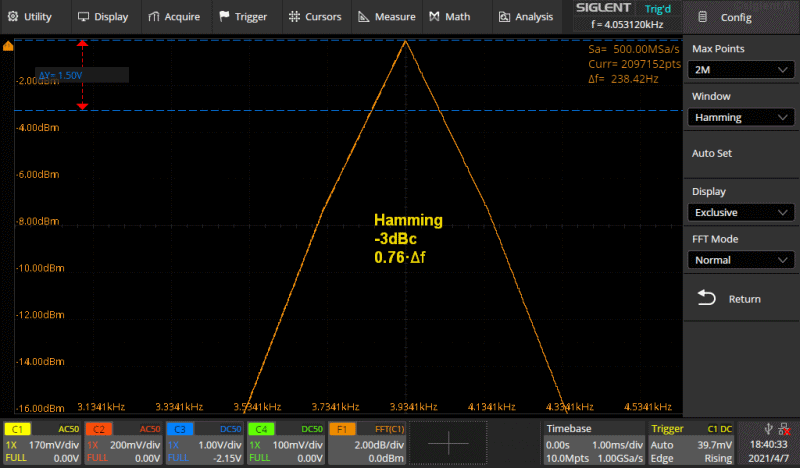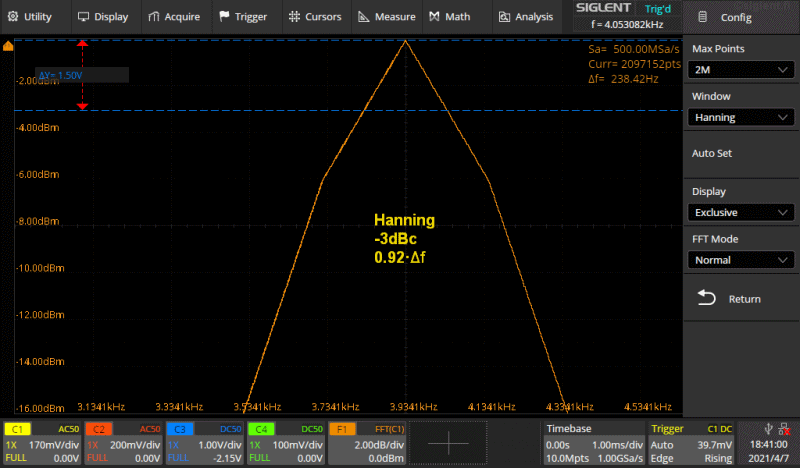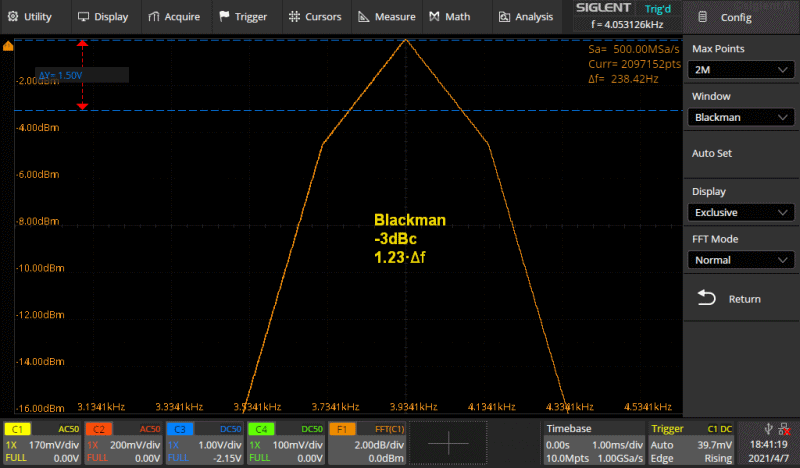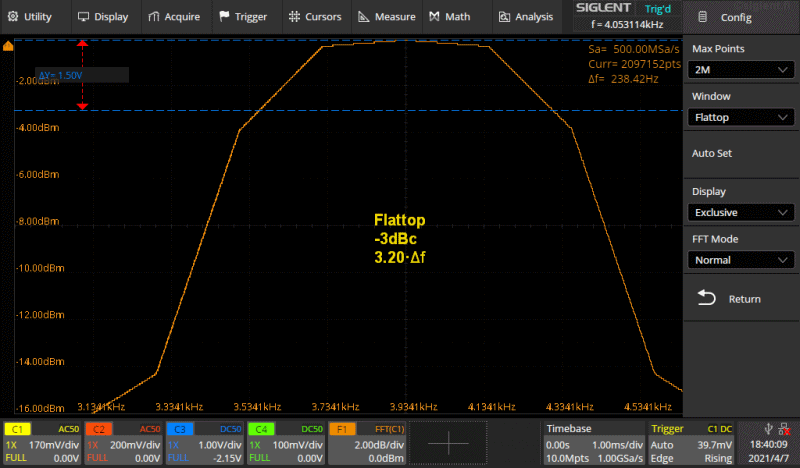
Kuva 5b. gif animaatio.
Kuvassa on Rectangle ikkunaa lukuunottamatta käytössä olevat ikkunat, Hamming,
Hanning, Blackman sekä Flattop peräkkäin. Asetukset on tarkoituksellisesti
asetettu siten että tuo muoto tulee kunnolla näkyviin. Asetukset vertikaali
asteikkoa lukuunottamatta samat kuin Kuvassa 5a.
Kuvassa 5b siis suntaa antava leveys -3dBc tasolla jolla tasolla on sininen
kursori (älä välitä kursorin jännitearvoista, sillä ei ole mitään merkitystä, ne
katkoviivat ovat vain kuvassa selkeytämässä asiaa).
Nyt kun ajattelet että tutkittava taajuus voi olla jossain muuallakin kuin juuri
niissä taajuuspisteissä jotka ovat Δf kerrannaisia eli osuvat johonkin
niiden välille syntyy tasovirhettä. Tason osalta aivan ylivoimaisesti paras on
Flattop jota on hyvä käyttää aina kun tasotarkkuutta tulee olla, seuraavaksi
paras on Blackman joka antaa myös paremman erottelukyvyn kun tarkastellaan
toisiaan hyvin lähellä olevia taajuuksia.
Tasovirhe syntyy seuraavan kaltaisesti kun tutkittava osuu bin väliin.
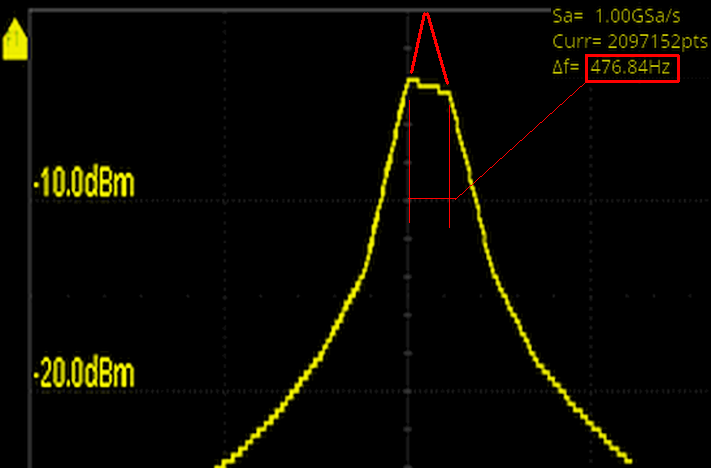
Kuva 5c (kuvaa on leikelty, kaikki epäolennainen pois, mutta asiat on
oikein)
Yllä esimerkki siitä mitä tapahtuu kun tutkittava taajuus ei osuu kohdalle.
Tuossa taajuus on osunut "väliin". Tuossa on yksi taajuuspiste suunnilleen
tuossa keskilinjalla ja seuraava siitä 476Hz eteempäin kyseisellä resoluutiolla.
Tutkittava on hiukan lähempänä keskilinjan pistettä kuin seuraavaa.
Mikäli tuo olisi mitattu Flattop käyttäen virhe olisi "olematon" ja myös
Blackman ikkunalla melko vähäinen. Tuo on tehty Rectangle ikkunalla jolla ilmiön
saa oikein erittäin selvästi esiim. Rectangle ikkunan scallop loss on
suuruuslukkaa lähes 4dB.
Huomioi siis tästä syystä johtuva mahdollinen tasovirhe joka tulee huomoida
kaikilla muilla paitsi Flattop filtterilla. Toki muut tasovirheet sitten
erikseen.
Tämä sama voi esiintya aika kiusallisestikin esimerkiksi katsellessa AM
moduaaltion sivunauhoja jollain muulla kuin Flat top filtterillä. Jos ne ovat
eri tasolla syyhän voi olla aivan skoopin ulkopuolella mutta se voi olla nyt
tämän FFT aiheuttama. Jos ne ovat eri tasolla muuta ensin FFT ikkuna Flattop
ikkunaksi ja jos edelleen virhettä, sitten vasta siirry muiden syiden
jäljittämiseen.
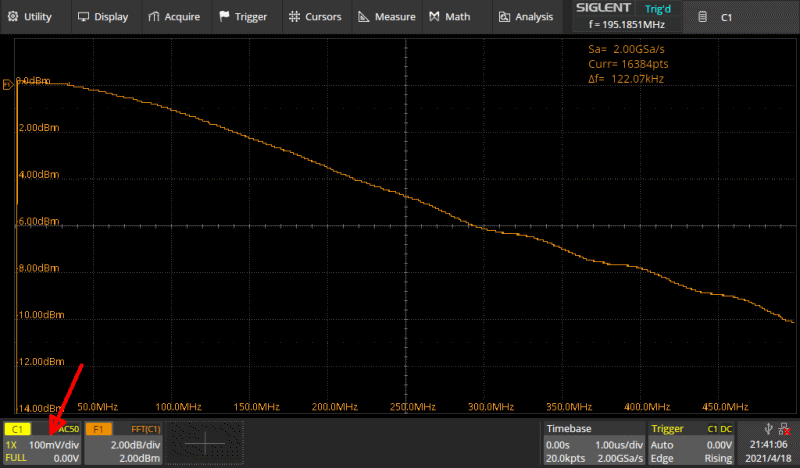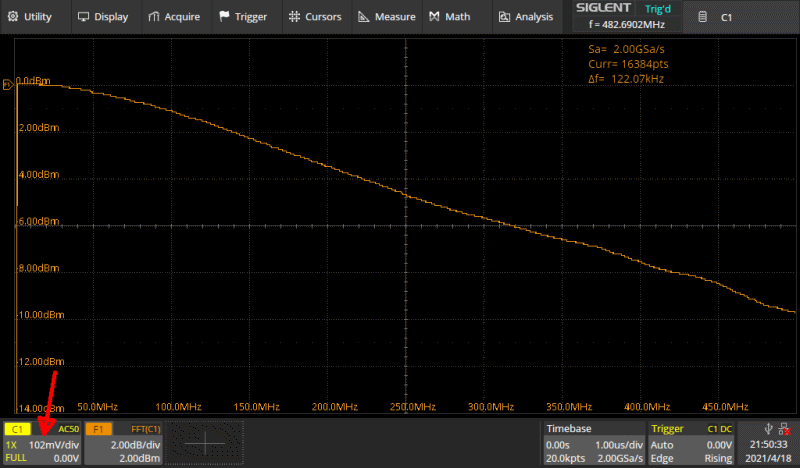
Tässä on pieni esimerkki FFT käytöstä. Kyllähän silläkin eräänlaisen bodeplotin
saa aikaan.
Jatkku, under construction...
Seuraavaksi hiukan FFT asetusvalikoista ja jokin esimerkki asetusten teosta.
Tähän piti tulla aiheesta mutta valitettavasti minulla ei ole tällä hetkellä
käytettävissä SDS2000X Plus mallia joten tältä osin korvautuu SDS2000X HD malli
kanssa tehtynä.
Sinänsähän asiat ovat samoja olkoot malli mikä tahansa. Asetusvalikot jne voi
olla eri mutta kyllä ne pääasiat ovat ihan samoja. Toki jotain toimintoja voi
olla enemmän tai vähemmän mallista riippuen.
SDS2000XPlus, SDS5000X ja SDS6000A ovat jossain mielessä samaa sukua ja varsin
paljon samankaltaisuutta vaikka sitten suoritusrvot ovatkin erilaiset ja
toiminnoissakin on eroja mutta softallisesti samaa perhettä.
SDS2000X HD on kuitenkin erittäin paljon samanlainen FFT toimintojen
suhteen. SDS2000X HD FFT.
--» Ylös
--» Oskilloskoopit
--» Etusivulle - Home