 Oskilloskoopin valinnan kriteereitä
Oskilloskoopin valinnan kriteereitä Oskilloskoopin valinnan kriteereitä
Oskilloskoopin valinnan kriteereitä
Oskilloskoopin valinta ei ole aina helppoa.
Seuraavassa joitain perustietoja sekä näkemyksiä valinnan pohjaksi perusasioiden
osalta. Ennen muita ominaisuuksia pitää selvittää ensin muutama perusasia.
Huomaa että tämä artikkeli on osin vanhentunut uusien oskilloskooppimallien myötä.
Tietenkin yhtenä valintakriteereinä on hinta.
Mikäli on melko rajattomasti rahaa käytettävissä, asia
on erittäin yksinkertainen. Siinä ei paljoa ns älyllistä pohdiskelua tarvita.
Ostaa reippasti yli sen minkä tarvitsee nyt ja hiukan vielä ns tulevaa varten
marginaalia. En kuitenkaan puutu hintakysymykseen valintakriteerinä tässä
oikeastaan lainkaan. Kun halutaan onnistua rajallisella budjetilla
mahdollisimman hyvin on alettava pohtia ja "optimoida" useita seikkoja. Mieti
tarkkaan mitä teet oskilloskoopilla ja luo siitä käsitys sellaisdista
vaatimuksista joista ei voi tinkiä, sitten sellaiset joista voi tinkiä ja sitten
ehkä päälle saattaa tulla niitä "ihan kiva olla jos mahdollista" ominaisuuksia.
Kuitenkin vaikka oskilloskoopissa olisi mitä tahansa toinen toistaan hienompia
"wow" ominaisuuksia, niillä ei tee oikeastaan mitään ellei perusasiat ole
kunnossa. Yli kaiken muun ensimmäinen asia on tarpeellinen kaistaleveys
(taajuusalue) ja tarpeellinen näytenopus (samplenopeus) joka liittyy erittäin
läheisesti näytemuistin määrään. Jos ne eivät riitä tarpeeseen, on kaikki muu
oikeastaan turhaa eli skoopista tulee lähinnä silloin leikkikalu tai koriste.
Koska oskilloskoopit kehittyvät koko ajan ja jotkin mallit jäävät historiaan on
hyvä huomata että silti nämä perusteet pysyvät mutta esimerkiksi Sin(x)/x
interpolointi on voinut kehittyä paljonkin muun muassa lisääntyneen
käytettävissä olevan prosessointitehon ansiosta.
Koska tämän alkuperäisen vuosia vanhan tekstiversion jälkeen on esimerkiksi
Siglentin tuotevalikoimassa tapahtunut huomattavia muutoksia, muutama sana
siitä.
Vuonna 2020/2021 ja edelleen 2022 sanon että lähes jokasen harrastan tarpeet tulevat
tyydytetyiksi jollain seuraavan ryhmän mallilla.
Eivätkä ne ole ainoastaan harrastajan oskilloskooppeja. Tietenkin ne soveltuvat
myös ammattikäyttöön sekä ominaisuuksiltaan että laadultaan.
SDS1104X-U 4 kanavainen 100MHz 4 kanavainen mainio ja suht edullinen
skooppi.
SDS1000X-E 2 ja 4 kanavaisia 100 - 200MHz.
SDS2000X Plus. 2 ja 4 kanavaisia 100 - 350MHz (500MHz)
Näistä SDS1104X-E sekä SDS2104X Plus ovat todella erittäin suosittuja ja
monestakin syystä.
Vuonna 2023 on edelleen saatu mukaan myös 12 bittinen SDS2000X HD sarja.
Ja hiukan aiemmin vaativaan käyttöön soveltuva SDS6000A mallisarja.
Ja lisää on luvassa...
Oskilloskooppia hankkiva pohtii usein kysymystä oskilloskoopin taajuusalueesta. Samoin näytteenottonopeus sekä muistin määrä askarruttaa. Aloitetaan ns nyrkkisäännöillä joihin kuhunkin otetaan sitten hiukan lisää syvyyttä.
Ennen nyrkkisääntöjä ja tarkempaa tarkastelua voisi sanoa että tavallisen elektroniikan
perusharrastajan minimi tai sopiva on nykyaikana 50MHz oskilloskooppi jossa on
vähintään 250MSa/s reaaliaikainen näytenopeus kaikille kanaville yhtaikaa. Tämä riittää melko laajalle
skaalalle perustason analogista ja digitaalista elektroniikkaa. Mutta rajat
tulee aika pian vastaan erityisesti mikäli signaalit ovat kanttiaalto/pulssi
tyyppisiä. Mutta aihe
on laaja ja sitä tarkastellaan hiukan tarkemmin.
Joku saattaa sanoa, että eihän minun signaalit ole kuin 1 tai 10MHz, miksi
tarvisin 100MHz oskilloskoopin. Mikäli esitän kysymyksen että tarkoitatko vain ja ainoastaan puhtaita
siniaaltoja - siitä alkaakin sitten tielle tulla mutkia ja kiviä. Koitetaanpa hiukan
niitä mutkia selvitellä ja työnnellä kiviä pois.
Esitys perustuu omaan pitkäaikaiseen kokemukseen sekä muun muassa Tektonix, Agilent-Keysight, sekä R&S esityksiin.
Oheismateriaalina kannattaa tutustua esim:
Sin(x)/x
Interpolation: Agilent Technologies
Nyrkkisäännöt - "vitosen" säännöt:
Nyrkkisääntö 1. Kaistaleveys eli taajuusalue.
Suhteellisen tasotarkkoihin mittauksiin
(mikäli Gauss tyyppisellä taajuusvasteella ns -3dB piste on sama kuin
taajuusalueen yläraja eli se taajuus joka yleensä lukee oskilloskoopin
etupaneelissa.)
Oskilloskoopin kaistaleveys 3 - 5 kertaa mitattavan sinityyppisen signaalin taajuus.
Tavallinen katselu onnistuu vähemmälläkin.
Oskilloskoopin kaistaleveys MHz = 1000 .... 1750 / mitattava
nousuaika ns kun signaali ei ole sinityyppinen.
Nyrkkisääntö 2. Tarvittava oskilloskoopin nousuaika. (ellei erikseen mainittu, 10/90% säännöllä)
Suhteellisen tarkkoihin nousuaikamittauksiin
Oskilloskoopin nousuaika 5 kertaa nopeampi kuin mitattava signaalin nousuaika.
-Tämä kulkee aika tavalla käsi kädessä tarvittavan kaistaleveyden kanssa.
Nyrkkisäännöt 3a. 3b. ja 3c. Tarvittava näytenopeus. (sample nopeus)
3a. Siniaalto tyyppiset signaalit.
Näytetaajuus mitattavan siniaallon taajuus x 5
mikäli Sin(x)/x interpolointi.
Näytetaajuus mitattavan siniaallon taajuus x 15 mikäli lineaarinen interpolointi.
3b. Nousuaikojen mittaukset esimerkiksi "kanttiaalto" signaaleista (10/90% säännöllä)
Kun tiedetään millainen on nopein nousuaika joka esiintyy
mitattavassa signaalissa ja joka halutaan mitata kohtuullisella tarkkuudella.
Edellyttäen tietenkin että oskilloskoopin itsensä nousuajasta ei tule estettä.
Tarvittava näytenopeus GSa/s saadaan: 5 /
tRISE
(ns)
3c. Kanttiaallon tai suorakaideaallon pelkkä visuaalinen tarkastelu (ei mittauksia)
Kun vain katsellaan kanttiaaltotyypisen koko signalin
kuvaa ja halutaan että se edes muistuttaa kanttia jolla tasanko latvana...
Vähintään 5 näytettä
jokaista puolijaksoa kohden, mieluummin 10. Jos
kyseessä on suorakaideaalto, jossa toinen puolisko on lyhyempi kuin toinen,
silloin mennään se lyhyemmän mukaan.
Suorakaideaallon (tai pulssin) osalta lasketaan lyhyemmän osan ajallisen
pituuden (tSHORTHALF) perusteella.
Siis olkoot jakso kuinka pitkä tahansa sille lyhyemmälle osalle 5
näytettä, tai mieluummin 10.
Vähimmäis samplenopeus GSa/s saadaan: 5
/ tSHORTHALF
(ns)
Jos siis lyhimmän suorakaideaallon osan pituus on 10ns riittää katselussa
0,5GSa/s. Vielä se ei tietenkään
näytä alkeisoppikirjan "ideaalilta" suorakaideaallolta mutta. Mieluummin kuitenkin olisi 10
näytettä eikä sekään ole paljon.
10 näytteen määrä tasajakoiselle puolijaksolle johtaisi välillisesti käytännössä
seuraavaan:
Jos jakson pituus olisi 20ns tarkoittaisi se kanttiaaltoa jonka taajuus on
50MHz.
Tällöin olisi 10 / tSHORTHALF
(ns) joka aiemman mukaan edellyttäisi vähintään 1GSa/s
näytenopeutta.
Henkilökohtaisesti vielä tuplaisin tuon. Tietenkin sääntö 3b on syytä pitää
mielessä.
Tässä on hyvä huomata että samalla on seurattava toista sääntöä eli
kaistaleveyttä.
4. Oskilloskoopin muisti.
Oskilloskoopin muistilla tarkoitan sen muisin pituutta
johon AD muuntimelta tulevat näytteet tallennetaan ennen käsittelyä. Usein juuri
se oskilloskoopin esitteissä kerrotaan. Tähän voisi antaa nyrkkisäännöksi. Niin
paljon kuin mahdollista, kuitenkin huomioiden sen kuinka laite käyttää muistia.
Monesti jo 1-4M alkaa riittää kanavaa kohti mutta lisä ei ole pahasta mikäli
oskilloskooppi käyttää viisaasti muistiaan. Lisäksi on syytä myös vielä nykyisinkin
tarkistaa onko myös pidempi muisti ns täysnopeaa.
Nyrkkisääntö. Ei alle 1M/kanava. Mieluummin yli 5M/kanava.
Älä aliarvioi samplemuistin määrän merkitystä!
Älä myöskään yliarvioi sitä. Aina ei enemmän olekaan parempi. Tässä kohden
sitten vaikuttaa se kuinka oskilloskooppi kulloinkin käyttää muistia.
Katsotaan nyrkkisääntöjä vähän tarkemmin, kokonaisuus on loppujen
lopuksi aika kompleksinen.
Asia ei ole noin yksioikoinen kuin nuo nyrkkisäännöt antaa ymmärtää.
Mutta nyt sitten varoituksen sana. Älä ajaudu hifistelemään liian tarkasti. Jos
oskilloskoopin on pakko vakavissa mittauksissa täyttää tietyt
tarkkuusvaatimnukset on laskettava tarkasti ja laajemmin minkä lisäksi asetetaan
ns "varmuuskerroin" ja valitaan oskilloskooppi tai muu mittalaite joka täyttää
"varmuuskertoimella" korjatut vaatimukset eli jonkun verran tiukemmat
vaatimukset.
Tietenkin toinen tapa on vain
yksinkertaisesti hankkia laite joka varmasti ja aina täyttää kaikki vaatimukset.
Se tapa
on helppo mutta kallis.
Joka tapauksessa kannattaa kirjata vaikka lyijykynällä ruutupaperille ne omat vaatimukset jotka on
valmiiksi tiedossa ja katsoa että vähintään ne reunaehdot täyttyy. Niiden osalta
kannattaa olla ankara. Jos niiden kohdalla sitten valintaa tehdessä lipsuu ja
joustaa on se myöhemmin seinä johon törmää. Jos siis tiedät että haluat
mitata 3ns nousnopeuksia siten että mittausvirhe ei ihan näistä perus asioista
tarkastellen ylitä 10% niin älä kuvittele että voit sen "jotenkin" tehdä
500MSa/s 100MHz oskilloskoopilla. Ei siihen riitä edes 200MHz. Ei vaikka
sille luvataankin nousuajaksi 1,75ns. Silloin tulisi valita 250MHz tai
mieluummin 300MHz oskilloskooppi. Miksi, se valottuu kohta.
Nyrkkisäännöt hiukan laajemmin tarkasteltuna.
Nyrkkisääntö 1. Suhteellisen tasotarkkoihin tarkkoihin mittauksiin
kaistaleveys 5 kertaa mitattavan sinityyppisen signaalin taajuus.
Jos tutkit
signaalia jonka taajuus on 100MHz ja signaali
on jatkuvaa melko puhdasta
siniaaltoa on tilanne aika yksinkertainen. Tarvitset oskilloskoopin jonka
kaistaleveys on 100MHz
- mutta vain siinä erikoistapauksessa ja vain jos signaalin tason tarkkuudelle
riittää mahdollisen virheen suuruusluokka 30%.
Oskilloskoopin nimellinen kaistaleveys tarkoittaa luonnollisestikin aina
siniaaltoa. Muuta se ei käytännössä voisi olla.
Kaistaleveys määritellään usein niin että asetetaan referenssiksi jokin
matalahko taajuus ja asetetaan sen tasoksi jokin ja "sovitaan" että tuo on
vertailusignaali ja sen taso on dB asteikon 0 kohta johon sitten verrataan ja
ero siihen ilmaistaan desiBeleinä koska Bel olisi liian suuri käyettäväksi.
Referenssitaso voisi olla esimerkiksi 600mV huipusta
huippuun. (muodoltaan puhdas siniaalto jolle ilmoitetaan myös taajuus,
esimerkiksi 10kHz tms, kunhan se vaan ilmoitetaan jotta mittaukset ovat
vertailukelpoisia).
Asetuksella 100mV/div signaali on
korkeudeltaan 6 ruutua (div) oskilloskoopin näytöllä. (Perinteinen ja
vakiintunut tapa kun näytön maksimi korkeus on 8 ruutua).
tapa 1. Nostetaan
signaalin tasoa 3dB ja nostetaan taajuutta kunnes signaalin korkeus on pudonnut
takaisin 6 ruudun korkuiseksi. Sillä taajuudella meillä on -3dB piste.
tapa 2.Voidaan tehdä myös niin että pidetään signaalin taso samassa kuin se oli
referenssitasoa mitatessa. Nostetaan vain taajuutta kunnes signaalin taso on
pudonnut noin 30% eli tarkemmin sanoen arvoon 0.708 * referenssitaso eli nyt noin 4.25 ruutua.
Luonnollisesti mittaus edellyttää että signaali saadaan tasotarkasti
oskilloskoopin tuloliittimeen (Siitä pisteestä sen taso tulisi mitata). Näinhän ei useinkaan ole.
Usein se katsotaan vain siitä mitä lähtee signaaligeneraattorista. Testaajan arvioitavaksi jää se kuinka luotettavana mittausta voi pitää.
Taajuuden kasvaessa vaikeusaste lisääntyy olennaisesti. Jo 100MHz
oskilloskoopin kanssa asia on kaikkea muuta kuin helppo mikäli pyritään alle 1dB
todelliseen tarkkuuteen. Taajuuden kasvaessa impedanssisovituksen laatu yms
alkaa vaikuttaa paljon. ON aivan varma ettö mikäli 300MHz oskilloskoopissa
on 1Mohm/15pF tulot ja siihen laitetaan T haaralla signaali ja T haaran yhteen
piippuun 50 ohm päätevastus on tilanne kaikkea muuta kuin ideaalinen varsinkin
siellä 300MHz tuntumassa. Ns feed thru eli läpi menevä päätevastus ei sekään
pelasta tilannetta vaikka onkin edellistä parempi. Miksi. Koska sen
päätevastuksen skoopin puolella on reaktanssi, sekä induktiivista ettö varsinkin
kapasitiivista reaktanssia sekä päälle se resistanssi joka on lähes
merkityksetön.
Alla muutama dB arvo. (esim.: Jos vertailutasosta 1V on pudotettu tasoon 0.316V on
pudotusta 10dB.)
| Taulukko 2 | ||||||
| -1dB | -2dB | -3dB | -4dB | -5dB | -6dB | -10dB |
| 0,891 | 0,794 | 0,708 | 0,631 | 0,562 | 0,501 | 0,316 |
Oskilloskoopin kaistaleveyden jatkeeksi pitää myös käsitellä samaan asiaan
liittyviä muita seikkoja.
Kokonaisuuteen jolla signaalia mitataan kuuluu itse oskilloskoopin lisäksi se
kuinka signaali tuodaan tuloliittimeen. Usein, mutta ei aina, käytetään
oskilloskoopin mittaapäätä - probea.
Toinen tapa on tuoda signaali
välikaapelilla jonkin tutkittavan laitteen liittimestä. Tällöin on huolehdittava
impedanssisovituksesta tuon siirrron osalta. Kun mennään taajuuksissa ylöspäin
alkaa monet seikat vaikuttaa. Ei tarvi kuin katsoa reaktanssikarttaa.
Esimerkiksi oskilloskoopin tulon 20pF kapasitanssin reaktanssi taajuudella 50MHz
on noin 160 ohmia ja 100MHz luonnollisesti puolet siitä jne! Mitä ihmettä,
sen tulonhan piti olla 1 Mohm... niin se onkin - tasajännitteellä!
Kaistaleveyden lisäksi myös taajuusvasteen muodolla
on merkitystä. Useinmiten edullisemman pään ja alle 500MHz - 1GHz
oskilloskoopeissa taajusvasteen muoto on "Gauss" tyyppinen. On myös
olemassa esimerkiksi mahdollisimman tasainen ("maximum flat") nimellistaajuuteen
saakka ja sen jälkeen jyrkkä pudotus (Tällöin joskus puhutaan myös "brick wall"
tyyppisestä vasteesta).
Taajuusvasteen muodossa saattaa olla myös mutkia ylös ja
alas eri taajuuksilla. Niiden on kuitenkin pysyttävä määriteltyjen rajojen
sisällä. Joskus rajat ovat melko väljät. Jos maininta on +/- 3dB 0-100MHz
ja referenssitaajuudeksi mainitaan esimerkiksi 1kHz voi vain kuvitella kuinka
järkyttävä taajusvasteen muoto voisi olla sen edelleen sopiessa tuohon +/- 3dB
ikkunaan.
Kun sitten ilmoitetaan myös vertikaalinen tarkkuus ja siellä sanotaan
esimerkiksi 3% pitää huomata se että sen lisäksi tulee tuo taajuusvasteen virhe.
Pahimmillaan -3dB joka vastaisi noin -30%. Älä siis odota että voisit luottaa
siihen että mittaamasi 10MHz siniaalto tasoltaan 1Vpp olisi samalla
tasoilla todellisuudessa sen mittaamasi 100MHz signaalin kanssa jonka tasoksi
oskilloskooppi näyttää myös 1Vpp. Lisää virhettä tulee sitten mittapäistä tai
muuten skoopin ulkopuolela. Oskilloskooppi EI pääsääntöisesti sovellu
tarkkoihin tasomittauiksiiin erilaisten signaalien välillä. Se on
kokonaan väärä väline siihen. Se onsignaalin muotojen havainnointiin ja
signaalissa tapahtuvien muutosten havainnointiin ajan suhteen. Sopivin
menetelmin voi toki suhteellisia tasomittauksiakin tehdä ja tason monitorointia
esimerkiksi monotoroituia signaalia säädettäessä. Kun se putoaa säätäessäsi
oskilloskoopin mukaan 6 voltista 5 volttiin voit olla melko varma että se on
pudonnut noin voltin. Mutta et oikeastaan tiedä onko sen taso alunalkaen 6V vai
9V vai 4V jos se on 100MHz skoopilla katseltu 100MHz signaali varsinkin jos
siihen on kytkeydytty tavallisella halvalla mittapäällä jollainen yleensä tulee
skoopin mukana.
Seuraava kuva antaa suuntaa taajuusvasteen
muodon osalta.
Siglent SDS1000X sekä SDS2000X oskilloskoopeissa on Gauss tyyppinen taajuusvaste
kuten on tavanomaista alemman taajuusluokan oskilloskoopeissa yleisesti.
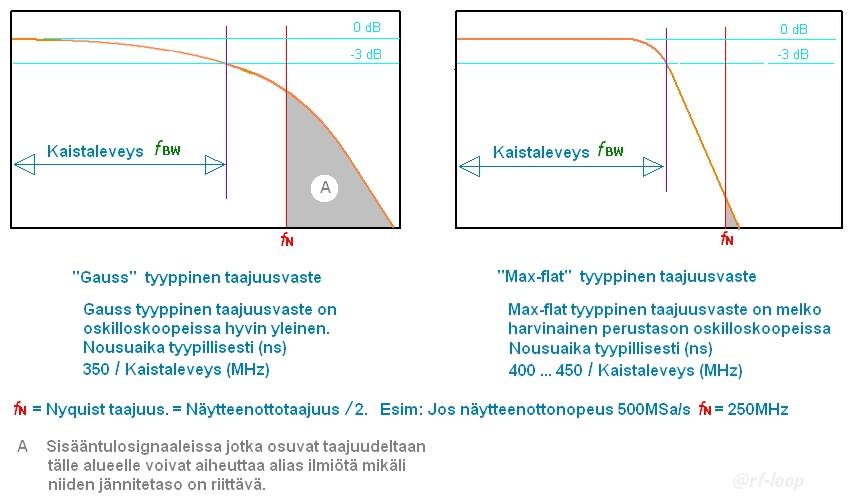
Kuva 1.
Mikäli oskilloskoopilla jossa on Gauss tyyppinen taajusvaste halutaan tehdä
mittauksia joissa signaalin jännitetaso on mahdollisimman oikein tulee
oskilloskoopin nimellinen kaistaleveys
fBW olla huomattavan korkea verrattuna mitattavaan
taajuuteen.
Mikäli tasotarkkuutta pitää tärkeänä on hyvä muistaa
nyrkkisääntö viisi ihan kuten nyrkissä on sormia. Mitattava taajuus
fBW / 5.
Mitattava taajuus * 5 on sopiva oskilloskoopin
fBW.
Tämä on myös esimerkiksi Tektronix sekä HP/Agilent/Keysight näkemys
"nyrkkisäännöksi". Mikäli oskilloskooppi on ns "maximal-flat"
tyyppisellä taajuusvasteella on tilanne tietenkin toinen.
Tarkempi asian tarkastelu edellyttäisi tarkkaa kuvaa oskilloskoopin
taajuusvasteen muodosta ja virherajoista. Kuvan 1. Gauss tyyppinen taajuusvaste
esiintyy nykyaikaisissa oskilloskoopeissa kohtalaisen harvoin ja jos esiintyy
niin lähinnä aivan edullisimman pään oskilloskoopeissa. Erittäin usein
todelolinen kaistaleveyden -3dB piste on korkeammalla tai taajuusvasteen muoto
on sellainen että tasotarkkuus on parempi. Mikäli tasotarkkuus on hyvin
tärkeässä asemassa oskilloskooppia valitessa on se hyvä selvittää
mallikohtaisesti tarkemmin.
Mikäli tarvittavaa kaistaleveyttä määritellään esimerkiksi
pulssireunojen
nousu- ja laskuaikojen mittauksen pohjalta on asia toisenlainen:
Aika usein näkee ja kuulee ajateltavan että koska 100MHz skoopin nousuaika
on noin 3.5ns niin sillä sitten voi mitata sellaisia nousuaikoja. Pieleen meni.
Yksinkertaistetaan hiukan. Ajatellaan että mitattavan signaalin nousuaika on 3.5 ns
ja oskilloskooppina 100 MHz oskilloskooppi Gauss
tyyppisellä taajuusvasteella oskilloskoopin nousuaika olisi
350 / 100=3.5 (ns). Periaatteessa nousuajan mittausvirhe olisi noin 40%. Toisin
sanoen 350/mitattava nousuaika ns antaa kaistaleveydeksi taajuus MHz jolloin
mittausvirhe luokkaa 40%.
Siis jos mitattava signaalin nousuaika on 3,5ns ja oskilloskoopin oma
nousuaika on 3,5ns mittauksessa syntyvä virhe voi olla 40%. Edellyttäen edelleen
että nöytenopeus on niin suuri ettei sen johdosta synny merkittävää
lisävirhettä.
Yhteenveto joka olettaa oskilloskoopin taajusvasteen olevan Gauss tyyppinen ja
kaistaleveys perustuu todelliseen -3dB pisteeseen.
Noin 40% virheeseen päästään jos oskilloskoopin kaistaleveys MHz on 350 / mitattava nousuaika ns.
Noin 20% virheeseen päästään jos oskilloskoopin
kaistaleveys MHz on 500 / mitattava nousuaika ns.
Noin 10% virheeseen päästään jos
kaistaleveys MHz on 650 / mitattava nousuaika ns.
Noin 3% virheeseen päästään
kun kaistaleveys MHz on 950 / mitattava nousuaika ns.
Hiukan alempana aiheesta lisää. Nyrkkisääntöä 2. käsittelevässä kohdassa.
Perusteena Dr. Howard
W.Johnson "High-speed Digital Design – A Handbook of Black Magic."
Kun joku nyt yritti minua oikoa että olen liian pessimistinen....
Douglas Brooks "Rise Times and Harmonics: Introducing Mr. Fourier" antaa myös
jonkinlaisen nyrkkisäännön joka karkeasti on seuraava. Mikäli signaalin
nousuaika on RT voidaan sanoa että käytännössä suurin merkittävä taajuus on
1/(3*RT). No mitäs tästä seuraa. Ainakin helposti virheellinen päätelmä
jos sanottua soveltaa pikasilmäyksellä skoopin valintaan, jos ei ole
tarkkana. Katsotaanpas 2 nanosekuntilla.
1/(3*0,000000002) = 166666666,... (aikahan oli sekunteina joten vastauskin oli
Herzeinä). No aika äkkiä havaitsee että asiahan on juuri se sama nyrkkisääntö
joka lienee alunpalin muinaisuudessa lähtenyt Tektronixilta. Siellä vaan luku
333 on pyöristynyt luvuksi 350 jota on mukavampi käyttää. Douglas Brooks siis
esitteli vuonna 2011 pyörän uudelleen. Tuo ei muuta mitään sanottua.
Yksinkertaiasesti, nämä perusteet eivät muutu ajan kuluessa ja oskilloskooppien
muuttuessa 50 luvun putkiskoopista 2021 luvun moderneihin digitaaliskooppeihin.
Sanotaan se nyt tässäkin. Vaikka katselisit 10Hz tai 10MHz pulssia/kanttia
jossa signaalin itsensä nousuaika/laskuaika on esimerkiksi 3.5ns tarvitset aivan
vähintään ns 100MHz oskilloskoopin jossa näytenopeus on vähintään 500MSa/s.
Siitä näytenopeudestakin alempana. Lyhin pulssi jonka voit nähdä edes hitusen
trapetsoidina on tällöin noin 10ns eli sen huomaa että se ei ole puhdasta siniä
vaan ikäänkuin siniä josta latvat on hiukan litistetty. 10ns pulssi. Jos 10ns
pulsseja tulisi siten että pulssien väli olisi myös tuo minimi eli 10ns niin
meillähän olisi silloin 50MHz kanttiaaltoa. Sen siis erotat siniaallosta mutta
etpä sitten juuri muuta siitä tiedäkään.
Mutta tässä ohitettiin nyt kirkkaasti yksi aika kova
fakta. Jonka Brooks ohittaa koska hänhän ei puhukaan oskilloskoopin valinnasta.
Kahden nousuajan summa eli ryhmänousuaika:
trise =
SQR (( trise1 ^2) + ( trise2 ^2 ))
Jos olisi 3.5 ns tulevan signaalin nousuaika ja skoopin oma
3.5ns nousuaika onkin noiden kahden summa 4.95ns eli 5ns. Jos ryhmässä on
nemmän jäseniä niin sitten vaan lisää tuonne summaan noita ( trise2 ^2 ).
Hiukan mutkia oikoen ja pyöristellen 15ns pulssi ja vastaavasti 50%
pulssisuhteella eli kanttina jaksoaika 30ns. Tuon taajuus olisi 33.3MHz. 100MHz
skoopilla näkyisi jonkin näköistä pyöreäkulmaista signaalia ikäänkuin siniä
josta latvoja litistetty tmv. Nousuajankin voi mitata ja siinä on sitten iso
virhe eli mittaat vain skoopin näkemää ryhmänousuaikaa, sitä jonka ruudulla
näet. Ruudulla et näe tällöin tulevan signaalin todellista nousuaikaa.
Muista siis että pulssi-kantti tyyppisilla digitaalipiirien signaaleilla
oskilloskoopin nimellisen taajuuden on oltava paljon suurempi kuin signaalin
perustajuus. 10MHz kantti muuttuu siniksi kun sitä katsellaan 10MHz
oskilloskoopilla.
Lähde siis siitä mikä on kantin tai pulssin nousuaika! Älä
tuijota sen signaalin perustaajuuteen. Älä myöskään laske perustaajuuden
harmonisia tavalla josta usein kuulee eli 5., 7. tai 9. harmoninen pitää saada
mukaan (vaikka onkin totta tietyllä tavalla ).
Ajattelepa 1kHz kanttia. Miltä tuntuisi katsella sitä esim 5kHz tai 10kHz
oskilloskoopilla. Jos sen signaalin tuotti vaikkapa ikivanha hidas perus CMOS
logiikka ja nousuaika sattui kyseisessä koko kytkennässä olemkaan vaikka hihasta
ravisteltuna 25ns. Mitä tiedät siitä 5kHz oskilloskoopilla joka siis täytti sen
5. harmoninen säännön. No, suoraan sanen et oikeastaan mitään paitsi että jakson
aika on noin 1ms. 10MHz skoopilla voisit jopa mitata ja päätellä että nousuaika
ainakin alle 50ns.
Nykyaikaisilla digitaalisilla signaaleilla nousuajat ovat melko nopeita. 100MHz
oskilloskooppi on tarpeen jo ihan perustason "Arduino" hommissa.
Esimerkiksi Siglentin SDS1104X-U ja siitä hiukan
ylöspäin ominaisuuksissa SDS1104X-E voisi sanoa olevan minimitaso. Siitä
ylöspäin SDS2104X Plus on jo vasrsinaista herkkua ominaisuuksiltaan ja sen
taajuusvastekin on usein reippaasti yli 150MHz todellisuudessa vaikka onkin
"100MHz" nimellisesti. (minulla olevassa yksilössä aivan tehtaan paketista
180MHz -3dB BNC liittimestä.) SDS2104X Plus ja sen variantit 350MHz jopa 500MHz
saakka voi sanoa olevan kova laite hiukan vaativampaankin käyttöön.
Niin ja niiden kaikkien SDS2kXPlus varianttien hardware on täsmälleen sama
lukuunottamatta mukana tulevia probeja.
Mittaustulos on
kokonaisuuden summa kaikkine virheineen. Monesti niin että mittauksemme
aiheuttaa virhettä myös itse mitattavaan. Ei mennä siihen laajaan aiheeseen nyt
enempää.
Aina ei riitä että hankkii sopivan taajuuskaistaisen oskilloskoopin probeineen.
Mittaukset saattavat vaatia lisälaitteita joiden hinta saattaa yllättää.
Aktiiviset hyvälaatuiset RF- ja differentiaaliprobet eivät ole halpoja. Saattavat
helposti maksaa enemmän tai moninkertaisesti edullisen koko
oskilloskoopin hinnan. Moni ihmettelee sitä. Vastaus selviää kun yrität
tehdä oikeasti korkealuokkaisen aktiivisen RF proben tai differentiaali proben.
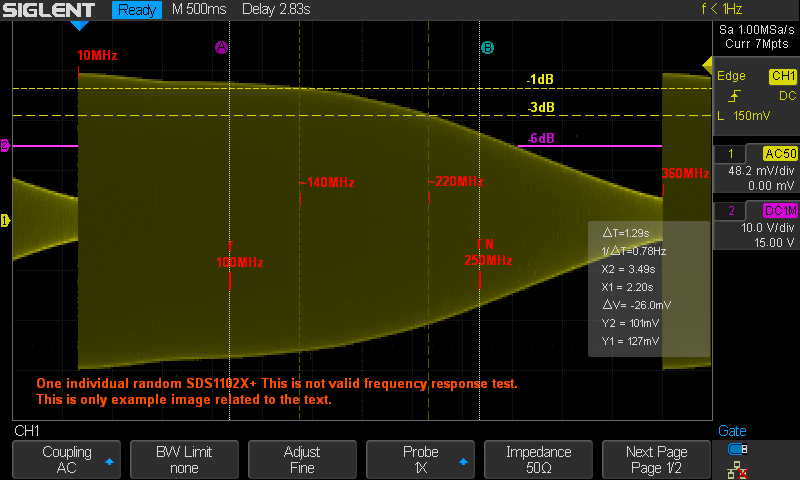
Kuva 2.
Esimerkkinä käytännöstä ja oskillokooppina SDS1102X (ei -E).
Kuva on vain
kuvituskuva. Siitä ei voi tehdä tarkkaa arviota taajusvasteen muodosta eikä
kaistaleveydestä. Mittauksen toteutus on siihen tarkoitukseen laadultaan puutteellinen. Kuvassa 2. on
piirretty fN
joka vastaa tilannetta silloin kun samplenopeus on 500MSa/s. Kuvassa näkyvällä
samplenopeudella ei ole mitään tekemistä tämän kanssa. Kyseessä on hitaalla
sweepillä toteutettu taajuusvastetta kuvaava verhökäyrä. vajaa 6 sekunnin ajalla
lineaarinen sweep taajuudesta 10MHz lopputaajuuteen 360MHz. 1 vaakaruutu vastaa
30MHz. A on kohdassa 100MHz. B on kohdassa fN.
Lisäksi on kursorit -1dB sekä -3dB kohdissa.
On enemmän sääntö kuin poikkeus että -3dB piste on reilusti
nimellistaajuutta ylempänä kun se mitataan oskilloskoopin tuloliittimestä. Siglent ei tee siinä poikkeusta ainakaan
alakanttiin.
Älä kuitenkaan odota että juuri sinun SDS1102X taajuusvaste olisi kuten kuvassa
2.
a Mittaus ei ole kelvollinen taajusvasteen mittaus.
b Oskilloskoopeissa on
yksilöeroja.
c Signaalilähteen ja oskilloskoopin välissä on siirtotie ja
impedanssisovitus enemmän tai vähemmän optimaalinen.
Karkeasti voisi sanoa että kyseisen mallin -3dB todellinen raja on 140MHz ja
180MHz välillä.
Silloin tällöin törmää myös siihen että oskilloskoopin taajuusvaste riippuu
valitusta jännitealueesta. Siglent oskilloskoopeissa, SDS1000X/X-E sekä
2000X/X-E sarjoissa on pyritty siihen että kaikilla herkkyys asetuksislla
taajuusvaste olisi kutakinkin sama.
Usein ja varsinkin analogisissa oskilloskoopeissa oli hyvin tavallista että
herkimmillä jännitelueilla oli taajusaluetta rajoitettu. Esimerkiksi Tektronix
50MHz 2225 jossa oli harvinainen 500uV/div alue, sen yläraja oli 5MHz.
Useissa digitaalisissa oskilloskoopeissa myöskin herkimmät alueet ovat jonkun
verran alemmalla taajuusvasteella ja joissain lisäksi jopa 2mV/div asetuksella
pakotetaan 20MHz filtteri päälle niin ettei stä voi edes kytkeä pois.
Esimerkiksi Siglent SDS1000X-E sarjassa 500uV/div on täyden resoluution ja
täyden taajuuskaistan mukainen. Toki kohinaa on. Ei nämä mitään fysiikan lakeja
riko ja niiden fysiikan lakien päällekin on vielä lisäksi kohinaa. Hyvin
matalakohinainen 1Mohm erittäin matalakohinainen etupää vaatisi nimittäin
melkoisia investointeja ja sittenkin vielä jäisi melkoinen terminen kohina.
Haluemme kuitenkin oskilloskoopin muutamalla satasella. Tässä hyvin
yksinkertaistetussa testissä kuitrenkin näkyy että V/div ei vaikuta olennaisesti
kaisteleveyteen.

Kuva 2a.
Kuvassa mittaustulos SDS1104X-E joka "on jotenkin muuntunut" SDS1204X-E
malliksi. (vastaa 1204X-E mallia)
Voi siis sanoa että läpi koko jännitealueen ei merkittävää muutosta
taajuusvasteessa. Toki jos alettaisiin "hifistellä" niin varmasti pieniä eroja
vastekäyrissäkin olisi varsinkin piirrettäisiin ne paperille jossa esim 1 ruutu
olisi joku desiBelin osa. Ei sellaisella hifistelyllä ole mitään todellista
käytännön merkitystä.
Nyrkkisääntö 2. Suhteellisen tarkkoihin nousuaikaittauksiin
oskilloskoopin nousuaika 5 kertaa nopeampi kuin mitattava signaalin nousuaika.
Huomioi myös ristiin tämän kanssa näytenopeuden vaikutus (
Nyrkkisääntö 3.b. ) suhteessa mitattavaan
nousuaikaan.
fBW on melko
läheisessä suhteessa myöskin oskilloskoopin itsensä ns nousunopeuteen. (rise
time, trise).
Mikäli oskilloskoopilla halutaan tehdä mittauksia signaalin nousu- ja
laskuaikojen suhteen ja tarkkuus on tärkeä on hiukan tutkittava faktoja. Taaskin tulee tuo viiden
nyrkkisääntö. Mitattavat nousunopeudet (trise) / 5
on tarvittava oskilloskoopin trise.
Nyt on huomattava että pelkkä oskilloskoopin nousuaika tai
taajuusvaste ei ratkaise. Välissä on usein esimerkiksi mittapää, probe.
Mikäli proben nousuaika on 3.5ns ja oskilloskoopin nousuaika on 3.5ns on
niiden yhteinen nousuaika noin 5ns. Tuo systeemin nousuaika voidaan laskea
seuraavasti: SQR (( trise1 ^2) + ( trise2 ^2 )).
Gauss tyyppisellä taajuusvasteella saadaan nousuaika nyrkkisääntömäisesti
laskemalla trise = 350/fBW
(Tulos saadaan ns kun taajuus annetaan MHz).
Gauss tyyppisellä taajusvasteella, jollainen on usein nykyajan digitaalisissa
oskilloskoopeissa, fBW
on reippaasti yli oskilloskoopin "nimen mukaisen" taajuuskaistan. Tällöin on
oskilloskoopin nousuaikakin usein hiukan parempi kuin valmistajan ilmoittama arvo.
Esimerkiksi Siglent SDS1102X mallissa -3dB piste on tyypillisesti alueella 140MHz - jopa 180MHz. (Kuva 2.)
Sen voi ajatella myös niin että sillä kompensoidaan mittaapään nousuaikaa joten
systeemin nousuaika on lähempänä "nimellistä" 3.5ns.
Myöskään Gauss tyyppinen taajuusvaste ei ole mitenkään tarkka Gauss. Ns
Max-flat tyyppisessä oskilloskoopissa nousuajat ovat tyypillisesti noin 15 - 30%
hitaammat mutta tasotarkuus nimellisellä taajuusaluella on tällöin parempi.
Gauss tyyppistä taajuusvastetta voisi luonnehtia siten että se on ikäänkuin kompromissi
nopeuden ja mittaustarkkuuden välillä.
Mikäli halutaan erityisen tarkkoja nousuajan mittauksia kasvaa oskilloskoopin
oman nousunopeuden merkitys. Mikäli 100MHz oskilloskoopilla (trise 3.5 ns)
mitataan 3,5ns nousunopeuksista signaalia on mittavirhe yli 40%. Noin 3%
mittavirheeseen päästäisiin jos oskilloskoopin kaistaleveys olisi lähellä
400 MHz.
Kuvassa 1. on harmaat alueet "A". On pidettävä mielessä että kaikki
taajuuskomponentit signaalissa jotka ovat suurempia kuin kuvan
fN ja jotka AD muunnin "näkee",
aiheuttavat alias ilmiötä. Kuitenkin jo reilusti alle taajuuden
fN alkavat
ongelmat. Käytännössä maksimi jollain tavalla käyttökelpoinen siniaallon taajuus
on fN/1.25
tai toisin sanoen sampletaajuus / 2.5 mikäli käytössä on
hyvin
toteutettu Sin(x)/x interpolointi. (syy yksinkertaistetusti
se että interpolointi on tehtävä hyvin nopeasti)
Katso kuva 3 alempana jossa ylimpänä juuri tämä 2,5 x
samplenopeus Sin(x)/x (käytetään myös nimeä Sinc) interpoloinnilla.
On huomattava että Sinc interpolointi voi olla kovin
monin tavoin toteutettu ja pienikin ero käytetyissä parametreissa voi
aikaansaada suuria eroja jotka näkyvät erityisen selvästi kun lähestytään
Nyquist taajuutta. Interpoloinnin osalta joudutaan tekemään kompromisseja koska
oskilloskoopilla pitää olla suhteellisen nopea vaste muutoksiin signaalissa.
Nyrkkisäännöt 3. a. b. ja c. Näytenopeus
(Samplenopeus, reaaliaika oskilloskooppi, kertapyyhkäisy eli "single shot").
Kun puhutaan digitaalisista oskilloskoopeista on samplenopeudella suuri
merkitys samoin kuin muun muassa tavalla interpoloida näytepisteiden
välit. Yleensä käytetään Sin(x)/x interpolointia (lyhyemmin Sinc). Voidaan myös piirtää pelkät
näytepisteet tai vetää suorat viivat peräkkäisten näytepisteiden välille. Ainoa
oikea todellinen data joka on saatu itse signaalista on kuitenkin se jono niitä
AD muuntimelta saatuja näytteitä. Se, ja vain se, raaka data.
Joissakin oskilloskoopeissa käytetty Equal Time tai "repetitive"
näytteenottotapa poikkeaa seuraavasta täysin mutta sellainen näytteenottitapa
soveltuu ainoastaan ns jatkuville signaaleille. En käsittele tässä sitä
lainkaan. Puhutaan vain ns reaaliaika oskilloskoopeista.
AD muunnin ottaa näytteitä signaalista ja antaa tasoa vastaavan binääriluvun
ulos. Tavanomainen AD muunnin oskilloskoopeissa on 8 bittinen. Useinmiten AD
muunnin toimii kiinteällä taajuudella, riippumatta siitä mitä oskilloskoopin
näyttö ilmoittaa samplenopeudeksi. Tämä nopeus on se millä näytteitä otetaan AD
muuntimelta edelleen muistiin, näytemuistiin. Jos AD muunnin on essimerkiksi
500MSa/s toimiva ja oskilloskooppi näyttää samplenopeudeksi 50MSa/s tarkoittaa
se sitä että muistiin otetaan näytejonosta joka kymmenes ja loput menevät
"bittiavaruuteen". Tätä kutsutaan desimoinniksi. Desimoinnin estämättä
myös hitailla sample nopeuksilla saattaa muun muassa triggauksen käytettävissä
olla koko nopeus ja jopa siitä generoitu "ylinäytteitys. Puuttumatta
yksityiskohtiin käyttäjää kiinnostaa pääasiassa tässä asiayhteydessä se mikä on
samplemuistiin tulevan datan "samplenopeus".
Siglent SDS1102X AD muunnin toimii yhden kanavan ollessa käytössä 1GSa/s
nopeudella. Voi ajatella että AD muunninn itsessään sisältää kaksi rinnan käyvää
500MSa/s muunninta jotka voidaan piirin sisäisesti yhdistää
toimimaan ikäänkuin yhtenä 1GSa/s muuntimena.
Nyrkkisääntö
3a.
(Signaali siniaalto)
Lisäys v 2023
HUOM! Monissa uudemmissa oskilloskoopeissa Sin(x)/x interpolointi
tai paremminkin Sinc "rekonstruktio" on kehittynyt ja allaolevat tiedot voivat
olla paljonkin muuttuneet.
Nykyisissä moderneissa oskilloskoopissa jossa on huomattava määrä enemmän
prosessointitehoa on myös Sinc usein parempi.
Esimerkiksi jos näytenopeus on 2.5x tutkittavan siniaallon taajuus on
rekonstruktio lähes täydellinen.
Huomaa kuitenkin että tutkittaessa muita kuin siniaaltoja tilanne on erilainen
ja tulee huomioida tutkittavissa signaaleissa esiintyvät ylimmät
taajuuskomponentit. (yksinkertaisimmillaan esim kanttiaalto)
Tämä artikkeli pohjautui suurelta osin aikaan jolloin oli juuri saatu
markkinoille SDS1000X-E mallin edeltäjä SDS1000X
Näytenopeus (samplenopeus) mielellään 3.5 - 5 kertaa ylimmän
mitattavan siniaalto signaalin taajuus mikäli käytössä on Sin(x)/x
interpolointi.
Mikäli käytössä lineaarinen interpolointi, 10 - 20 kertaa ylimmän mitattavan siniaalto signaalin taajuus
.
Seuraavaksi hiukan lisää tilanteesta jossa signaali on kohtalaisen lähellä
siniaaltoa. Kuinka samplenopeus vaikuttaa ja mikä riittää "kelvolliseen"
piirtoon käytännössä kun interpoloititapana on Sinc. Sinc interpoloinnilla
saadaan yleensä paras kuva signaalista varsinkin kun ollaan taajuusalueella
jossa jaksolle saadaan vähän näytettä AD muuntimelta. (1GSa/s
tuottaa 50MHz siniaallon yhdelle jaksolle 20 näyttetä)
Milloin samplenopeus on riittävä kun halutaan skoopin kuvaruudulla katsella
signaalia joka on suunnilleen siniaaltoa ja käytössä on kohtuullisen hyvin hoidettu Sinc
interpolointi.
Kun sanotaan samplenopeuden olevan 1GSa/s on siis näytteenottotaajuus 1GHz.
Kerroin tarkoittaa sitä
kuinka moninkertainen näytetaajuuden pitää ollaa tutkittavan signaalin taajuuteen
nähden, edellyttäen että signaali on kokolailla puhdaas siniaalto jotta
lopputulos on kuvatun kaltainen. Alempana oleva kuvasarja (Kuva 3.) näyttää mitä
se käytännössä voi tarkoittaa oskilloskoopin kuvaruudulla.
Seuraava taulukko 1. antaa osviittaa kun käytetään Sinc,
eli Sin(x)/x ,interpolointia ja signaalina on puhdas siniaalto:
Kerroin 2.5 vaivoin välttävä
"signaalin ilmaisuun" mutta aika "rumaa katsottavaa".
Kerroin 3.0 antaa jo "siedettävän" kuvan siniaallosta ja varauksin
käyttökelpoinen.
Kerroin 3.5 antaa melko hyvän tuloksen ja on jo varsin käyttökelpoinen hyvä.
Kerroin 4.0 on puhtaalle siniaallolle erittäin hyvä
Kerroin 5.0 tuloksessa on erittäin vaike havaita parannettavaa.
(tilanne luonnollisesti muuttuu olennaisesti mikäli ei puhuta siniaallosta ja
mitä enemmän siitä poiketaan.)
Huomaa että tulos riippuu myös Sinc interpoloinnin toteutuksesta ja siinä voi
olla valmistajakohtaisia sekä mallikohtaisia eroja. Oskilloskoopissa Sinc interpolointi on
toteutettava siten että sen taajuusvaste on siedettävä jotta reagoidaan
nopeisiin muutoksiin heti eikä kohta. Jos meillä olisi hyvin pitkä jakso
muuttumatonta siniaaltoa niin tietenkin voitaisiin saavuttaa hyvän näköinen
lopputulos aina erittäinkin lähelle Nyquist taajuutta - kunhan otetaan riittävän
pitkä näytejono ja aletaan laskea. Nyt ei ole sellaiseen aikaa vaan se on
tehtävä heti ja nopeasti. Tavan takaa näkee sellaisia esityksiä jotka toistavat
kuin papukaija sellaisia argumentteja, puhuessaan oskilloskoopin näytenopeudesta
ja taajusvasteista yms, että riittää kun taajuus on Nyquist taajuuden
alapuolella. Sanoisinko että siinä ollaan tulkittu Nyquist-Shannon
esityksiä jokseenkin puutteellisesti vaikka se kirjaimellisesti totta onkin
kunhan siihen lisätään ne muut ehdot jotka siihen aina kuuluvat.
| Taulukko 1. | |||||
| Samplenopeus | Kerroin 2.5 | Kerroin 3 | Kerroin 3.5 | Kerroin 4 | Kerroin 5 |
| (fNyq*1.25) | (fNyq*1.50) | (fNyq*1.75) | (fNyq*2.0) | (fNyq*2.5) | |
| 250MSa/s | 100 MHz | 83 MHz | 71 MHz | 62 MHz | 50 MHz |
| 500MSa/s | 200 MHz | 166 MHz | 142 MHz | 125 MHz | 100 MHz |
| 1GSa/s | 400 MHz | 333 MHz | 285 MHz | 250 MHz | 200 MHz |
Taulukko 1. sopii siniaallolle tai lähellä sitä oleville
signaaleille. Ajatellaan siis edelleen että haluat katsella 100MHz siniaaltoa.
Aiemmin selkisi että skoopin taajuusvasteen pitää olla 100MHz jotta sen taso ei
ole vaimentunut vielä kovin paljon. Mutta, 100MHz saa olla 100MHz skoopissa
vaimentunut jopa noin 30% verrattuna saman tasoiseen esimerkiksi 10kHz
siniaaltoon nähden. Usein esim 100MHz oskilloskoopeissa nykyisin -3dB piste on
paljon ylempänä ja 100MHz ei vielä ole vaimentunut lähellekään 3dB.
(tähän sopiikin sivuomautus: Koko systeemin taajuusvaste on se joka merkitsee.
Pitää huomioida probe tms + oskilloskooppi yhdistelman tajuusvaste.)
Jotta 100MHz siniaalto näyttäisi kohtuullisen hyvältä, ilman kovin häiritsevää tasojitteriä tai
"wobbleria" yms on nyt selvinnyt myös että samplenopeuden tulee olla vähintään
noin 350 - 400MSa/s. Aika monissa 100MHz oskilloskoopeissa samplenopeudet ovat 500MSa/s,
1GSa/s ja 2GSa/s. Jos otetaan Siglent SDS1000X sarjan oskilloskooppi, tarvitaaan
100MHz sinityyppisille signaaleille 100MHz malli. Silloin myös 100MHz sini on
melko hyvälaatuista vaikka käytössä on 2 kanavaa yhtaikaa. Silloin samplenopeus
on 500MSa/s kummallekin kanavalle. Mikäli käytössä on lineaarinen interpolointi
kerro taulukon kertoimet noin kahdella. Useat oskilloskooppien valmistajat
pitävät riittävänä kerrointa 2.5. Silloin vaan hyväksytään että tasojitteriä
esiintyy huomattavasti. Kuten alla ylin esimerkki.
Alla oleva kuva eri kertoimilla. Kuvassa käytetty asetuksia joilla
"opetustarkoituksiin" saadaan vaikutus selvästi esiin.
Esimerkiksi Siglent SDS1000X-E mallit pystyvät parempaan.
Lisäksi on huomattava että eräissä tapauksissa esimerkiksi zoomausta
käytettäessä saattavat jotkin parametrit prosessiin tulla pääikkunan t/div
pohjalta!
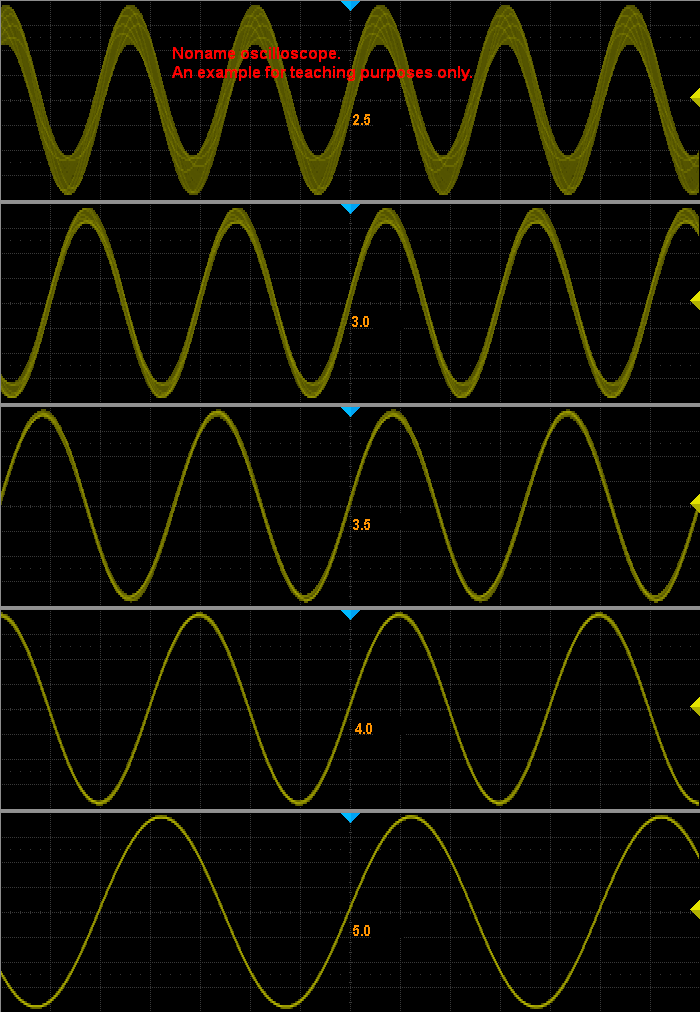
Kuva 3.
Kuvassa 3. sisään tulee siniaalto. Taajuudet kertoimen mukaaan. Kuvassa
samplenopeus (fSA
) on 50MHz
( 50MSa/s) sisään tulevan siniaallon taajuudet vastaavasti 20, 16.67,
14.89, 12.5 ja 10MHz.
Interpolointitapa Sinc. Jotta tilanne tulee paremmin esiin on käytössä myös 1s
"jälkiloisto" eli persistence.
Ero kertoimen 4 ja 5 välillä ei ole suuri. Kyseessä oli window zoom. Koko
ruudulla resoluutio on suurempi
ja ero tulee hiukan paremmin esiin. Kerroin 3.5 on edelleen ihan
asiallista katseltavaa.
Kuten havaitaan kerroin
2.5 on varsin kyseenalainen
muuhun kuin signaalin taajuuden summittaiseen määrittämiseen ja sen olemassaolon
havaitsemiseen.
Kerroin 3 hiukan parantaa asiaa ja on jo usein käyttökelpoinen. (huomaa että
ilmiö ei tule sekasignaaleilla
aina kovinkaan helposti esiin tai se saattaa sekoittua muihin seikkoihin itse
tutkittavassa signaalissa.
Nyrkkisääntö 3. b.
(nousuaikojen mittaus kun käytetään 10% - 90% sääntöä. )
Käytännössä tämä tulee rajoittavaksi aika harvoin mikäli nousuajan
mittaustarkkuudelle ei aseteta suuria vaatimuksia. Hyvin usein ensimmäiseksi
asiaa rajoittaa oskilloskoopin analoginen kaistaleveys.
Tarkista kuinka kaistaleveys vaikuttaa! (
Nyrkkisääntö 2. )
Ajatellaanpa esimerkiksi 100MHz oskilloskooppia jossa käytössä mittaukseen olisi
1GSa/s.
100MHz oskilloskoopin nyrkkisääntömäinen nousuaika on 3.5ns tavanomaisella
etupäällä.
Jos nyt mittaisimme signaalin 3.5ns nousuaikaa saisimme teoriassa 4.95ns
trise =
SQR (( trise1 ^2) + ( trise2 ^2 ))
Vaikka käyttäisimme 500MSa/s olisi kaistaleveys ongelma. Tosin kaistaleveys vain
rajoittaa nousuaikaa.
Sensijaan digitoinnin hidastuessa nousuaikaan nähden aiheuttaa se vaihtelua
nousuajan mittaukseen interpolointitavasta riippuen jota voi suodattaa
jatkuvilla signaaleilla keskiarvoistamalla.
Tarkkoihin nousuaikamittauksiin tarvitaan,
mikäli kaistaleveys riittää, vaadittuun tarkkuuteen:
5000 / mitattava nousuaika (ns).
Sin/x)/x interpolointi ei paljoakaan paranna tulosta. Myös
lineaarisella (vektori) saadaan tarkkoja tuloksia.
Tämä vastaa 5 näytettä nousuajan osalle.
Keskinkertaisen tarkkoihin nousuaikamittauksiin usein riittää
mikäli kaistaleveys riittää vaadittuun
tarkkuuteen:
3500 / mitattava nousuaika (ns.) Sin(x)/x interpolointi parantaa
tulosta mutta voi aiheuttaa pientä ylilyöntiä nurkissa.
Tämä vastaa 3.5 näytettä nousuajan osalle.
Suuntaa antaviin nousuajan mittauksiin mikäli
kaistaleveys riittää vaadittuun tarkkuuteen:
1750 / mitattava nousuaika (ns). Sin(x)/x interpolointi parantaa tulosta
mutta aiheuttaa ylilyöntiä nurkissa.
Tämä vastaa 1.75 näyttetä nousuajan osalle.
Erittäin epätarkkoihin nousuajan mittauksiin mikäli kaistaleveys riittää
vaadittuun tarkkuuteen:
1250 ~ 1500 / nousuaika (ns). Sin(x)/x interpolointi parantaa tulosta mutta
aiheuttaa voimakasta ylilyöntiä nurkissa.
Tämä vastaa 1.2 ~ 1.5 näytettä nousuajan osalle.
Alle 1200 / mitattava nousuaika (ns) ei tule käyttää nousuaikaa koskeviin
arviointeihin. Tulokset kelvottomia.
Katso kuvat 4, 5, 6 ja 7
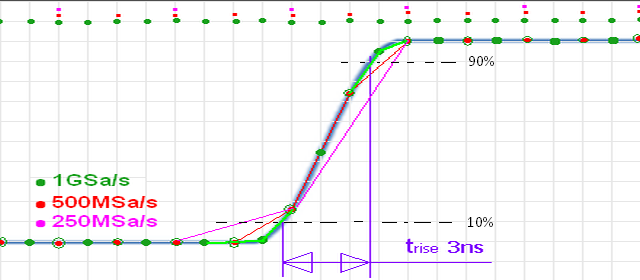
Kuva 4.
Esimerkki siitä miltä erilaiset näytenopeuden näyttävät tyypillisellä signaalin
nousevalla reunalla.
Kuten havaitaan tässä 3ns nousuajalle 250MSa/s on hyvin huono erityisesti kun
kuseessä on lineraarinen interpolointi. Tällä nopeudella myöskään Sinc
interpolointi ei enää tuota lainkaan kaunista tulosta. Sen sijaan 500MSa/s ja
Sinc interpolointi alkaa tuottaa jo katselukelpoista ja 1GSa/s tulos on jo
katselutarkoituksiin erinomainen.
Seuraavissa kuvissa on esimerkit käyttäen 1.25, 1.75 sekä 3.5 näytettä
sisääntulevan signaalin nousuajalle.
( trise 10/90% säännöllä)
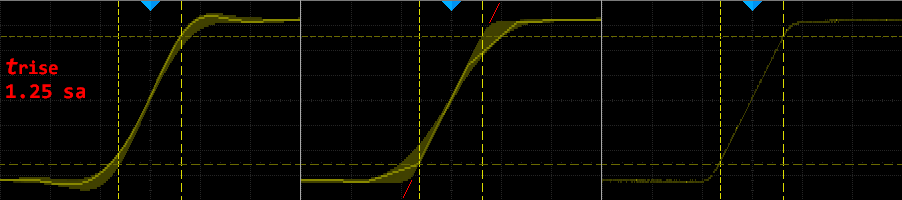
Kuva 5.
Kuvassa näytenopeus (MSa/s) on 1250 / signaalin nousuaika ns. ( 1250 /
25 = 50 ). Signaalin nousuaika 25ns ja 50MSa/s
Vasemmalla Sinc interpolaatiolla, seuraavaksi lineaarinen ja lopuksi pisteet.
Pisteiden osalta on hyvä huomioida se että yhdellä
vaakapyyhkäisyllä on tuotettu vain nuo kuvassa näkyvät kirkkaammat pisteet 20ns
välein. Kun vaakapyyhkäisyä toistetaan sijaitsevat
pisteet satunnaaisissa paikoissa siignaaliin nähden ja näin signaalista
muodostuu kuva (persistence käytössä).
Lineaari interpolaatioon liittyy piirre jota kannattaa tarvittaessa käyttää
hyödyksi. Huomaat kuinka punaiset merkit on piirretty kuvaan.
Kun persistence on käytössä piirtyy signaalin nousuaika melko oikein myös jopaa
näinkin alhaisella samplenopeudella. Otetaan siis
persistence jäljen osoittama nopein nousuaika. Lineaari interpolaatio voi
muulloinkin olla hyödyllinen, sen olemassaoloa ei pidä unohtaa.
Kuvassa kuitenkin nähdään että muuttumattimalle jatkuvalle signaalille saatetaan
saada kohtalaisesti määritettyä nousuaika mutta
"real time" tai "single shot" tyyppisesti nousuajan määritys on todella erittäin
epätarkkaa.
Vaikka kuvassa onkin käytetty 50MSa/s toimii tämä periaatteessa aivan samoin
500MSa/s tai 1GSa/s. Kuva on tehty matalalla
nopeudella jotta voin riittävällä tarkkuudella ja luotettaavasti säätää tulevan
signaalin nousuaikaa.
Kuvan tilanne vastaisi samaa kuin 250MSa/s samplenopeudella toimittaessa tulevan
signaalin nousuaika olisi 5ns ja oskilloskoopin
taajuusvaste muuten riittäisi tähän tarkoitukseen. Vastaavasti 500MSa/s tilanne
vastaisi sitä että sisään tulevan signaalin nousuaika olisi
2.5ns ja kun oskilloskoopin kaistaleveys olisi riittävä.
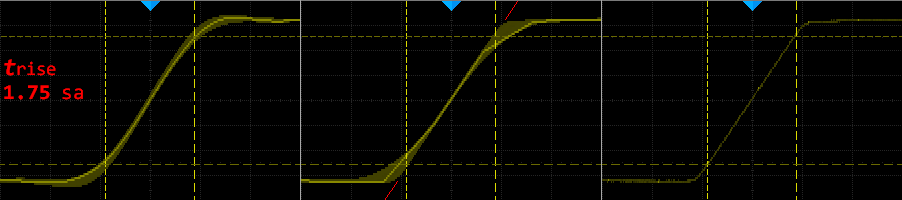
Kuva 6.
Kuvassa näytenopeus (MSa/s) on 1750 / signaalin nousuaika ns. ( 1750 / 35 = 50 )
Signaalin nousuaika 35ns ja 50MSa/s
Ks myös kuva 5. teksti. Nousuajalle saadaan nyt 1.75 samplea.
Tässä tilanne vastaisi samaa kuin samplenopeudella 250MSa/s sisään tulisi 7ns
nousuajalla oleva signaali tai 500MSa/s sisään
tulisi 3.5ns nousunopeuksinen signaali. Single shot tarkkuus ei ole hyvä mutta
antaa toki suuntaa nousuajalle.
Huomaa mikä on 10 ja 90% viivalla ajallinen vaihteluväli ja lineaari
interpolaation erikoispiirre kun persistence käytettävissä (merkitty kuvassa
punaisin viivoin).

Kuva 7.
Kuvassa näytenopeus (MSa/s) on 13500 / signaalin nousuaika ns. ( 3500 / 70 = 50
) Signaalin nousuaika 70ns ja 50MSa/s
Ks myös kuva 5. teksti. Nousuajalle saadaan nyt 3.5 samplea.
Tässä tilanne vastaisi samaa kuin samplenopeudella 250MSa/s sisään tulisi 14ns
nousuajalla oleva signaali tai 500MSa/s sisään
tulisi 7ns nousunopeuksinen signaali. Tai 1GSa/s sisään tulisi 3.5ns
nousunopeuksinen signaaali. Single shot tarkkuus on kohtuullisen
hyvä ja myös single shot tapauksessa saadaan hyvä käsitys nousuajasta.
Kuitenkin, edelleen havaitaan että virheen osuutta
on edelleen. On helppo päätellä että tarkka nousuajan mittaus edellyttää
nousuaikaan nähden varsin suurta samplenopeutta.
Karkeasti voisi sanoa että kun käytetään 7 näytettä nousuajan matkalle ei
samplenopeuden nostaminen siitä enää varsinaisesti
paranna tilannetta. Toinen virhelähde oli oskilloskoopin
kaistaleveyden vaikutus (ja taajuusvasteen muoto). On siis tehtävä
kompromisseja tai hankittava vaadittaavaan tarkkustasoon riittävä kaistaleveys
jolloin hyvin usein myös samplenopeus on
riittävän korkea.
Kuitenkin on hyvä muistaa että samassa mallisarjassa usein samplenopeus on sama
ja sitten kaistaleveyksiä on useita.
Esimerkiksi SDS1000X sarjassa länsimarkkinoilla mallit 100 ja 200MHz. 200MHz
mallissa nousuaika on < 1.75ns mutta
kaksi kanavaa samanaikaisesti käytössä samplenopeus 500MSa/s. Tässä sample
intervalli olisi pidempi kuin sisääntulevan
signaalin nousunopeus. 1GSa/s taas vastaisi samaa kuin kuvassa 6.
Nyrkkisääntö 3. c.
(kanttiaallon visuaalinen tarkastelu, ei nousuaikamittauksia)
Mikäli ei tarvitse mitata nopeita nousuaikoja mutta kanttiaalto
halutaan visuaalisesti näyttävän kanttiaallolta kuvaruudulla näytenopeus
vähintään 10 - 20 kanttiaallon (50% duty) perustaajuus.
Nyrkkisääntö 4. Muistin pituus.
Muistin määrä vaikuttaa aivan olennaisesti siihen millaisia näytenopeuksia
oskilloskooppi voi käyttää hitaammilla t/div asetuksilla ja se taas on usein
erittäin tärkeä asia.
Tämä oli aikaisemmin digitaalisten "reaaliaika"
oskilloskooppien ehkäpä pahin akilleen kantapää.
On edelleenkin usein kuultu asia että "en minä niin paljon muistia tarvi,
lähinnä katson signaaleita kuvaruudulta". Niin, vanhassa Hoo-Peessä tai
Tektronixissa saattoi olla esimerkiksi noin 500 tavua näyte- eli samplemuistia.
Ja hyvin näki 100 tai 500MHz. Niin näki. Niissä iskolloskoopeissa oli usein
kaksi eri toimintamuotoa, ns repetitive ja single shot. Koska AD muuntimet
olivat joka tapauksessa hitaita. Repetitive tyyppisesti voidaan vaikka 10MSa/s
AD muuntimella saada aikaan 100MHz oskilloskooppi tai vaikka 400MHz. Mutta,
signaalin pitää olla muuttumaton eli ns jatkuva, ja sitten odotetaan kun skooppi
rakentaa pikkuhiljaa kuvan signaalista.
Jos puhutaan reaaliaika oskilloskoopeista joissa nimenomaan yksi vaakapyyhkäisy,
single shot, riittää koko oskilloskoopin taajuusalueelle ja ajatellaan että
pskilloskooppimme olisi 200MHz malli ja näytenopeus max 1GSa/s.
Nyt jos sellasessa oskilloskoopissa olisi 500 tavun muisti olisi tilanne aivan
kaamea. Tietenkin jos aika asetus olisi 1ns/div niin luonnollisesti tuolla
muistilla, eli sillä vaakapyyhkäisyn max datapituudella, 1GSa/s kyetään ajamaan.
Mikäli kuvan leveys on sama kuin koko vaakapyyhkäisyn pituus ja jos kuvaruudun
leveys olisi perinteinen 10div tarkoittaisi se tuolla asetuksella sitä että
yhden vaakapyyhkäisyn pituus olisi 10 näytettä! Tuo 500 tavun muisti riittäisi
tuossa tapauksessa ajamaan vaikka 100GSa/s. Eli se ei rajoita.
Mutta, entäpä kun asetetaan nyt ajaksi 1us/div ja pysytään edelleen 1GSa/s
samplenopeudessa. Näytön leveys ja siis vaakapyyhkäisyn pituus olisi nyt
ajallisesti 10us. 500 tavun muisti olisi täynnä jo 0,5us kohdalla! Jotta nyt
kyettäisiin vaakapyyhkäisy tekemään kuvan keveydelle tulisi näytenopeuden olla
50MSa/s. Meillä olisikin nyt enää 25MHz oskilloskooppi. Entäpä jos pudotetaan
aika setus nopeuteen 1ms/s. Edelleen jouduttaisiin pudottamaan samplenopeutta.
Nyt se olisi enää 50kSa/s. Meillä olisi max 25kHz
oskilloskooppi.
Sen sijaan. Nyt jos samplemuistin pituus olisikin 5M tavua olisi mahdollista
ajaa samplenopeudella 500MSa/s ja meillä olisi edelleen 200MHz oskilloskooppi.
Vaikka 200MHz signaalia onkin melko hyödytöntä katsella 1ms/div asetuksella niin
siihen voisi sanoa että puhtaan 200MHz sinin katseleminen kuvaruudulta on
muutenkin aika tylsää. Sen sijaan mehän tutkimme muutoksia. 200MHz siniaallossa
voikin olla muutoksia jotka ovat ajallisesti ms luokkaa. Voisiko
yksinkertaisempaa esimerkkiä mainita kuin esim AM moduloitu signaali. Tai muiita
paljon mielenkiintoisempia esimerkkejä joita löytää niin virtalähteistä tai
vaikka vanhasta televisiosta.
Älä aliarvioi samplemuistin määrän merkitystä!
Mutta älä myöskään yliarvioi sitä. Aina ei enemmän olekaan parempi. Tässä kohden
sitten vaikuttaa se kuinka oskilloskooppi kulloinkin käyttää muistia.
Esimerkiksi Siglent SDS1202X-E ja muut SDS1000X mallit kykenevät
säilyttämään 1GSa/s näytenopeuden koko alueella 1ns/div - 1ms/div.
Seuraavassa kuvassa esimerkin vuoksi laskettu oletusarvoilla: Max samplenopeus
1GSa/s, samplemuistin pituus 20 t/div ajan ruutua. Muistin määriksi valittu: 1k,
10k, 100k, 1M, 10M ja 100M vaaka akselilla. Pystyakselilla t/div asetukset
1ns/div - 10ms/div yleisellä 1-2-5 askelluksella.ja niitä vastaavat
samplenopeudet kullakin muistin pituudella. Tämä riippuvuus suhde muistin
pituudesta ja mainituista muista seikoista on aivan sama valmistajasta
riippumatta. Se vaihtelee mikä on muistin pituus, kuinka säädellään
samplemuistin ajallista pituutta eli kuinka monta aika asetuksen ruutua tai siis
jako osaa on se piuus. Se ei voi alittaa kuitenkaan kuvaruudun leveyttä joka
sekin on valmistajakohtainen. Joskus Tektronix on kayttänyt tuota 20 div
leveyttä (kuvaruudun leveys 10 div kummallakin puolella 5div ylitys kuvan
ulkopuolella) Taulukko on tässä esimerkinä ja tarkoitus on vain helpoilla
lukuarvoilla selventää mistä on kyse.
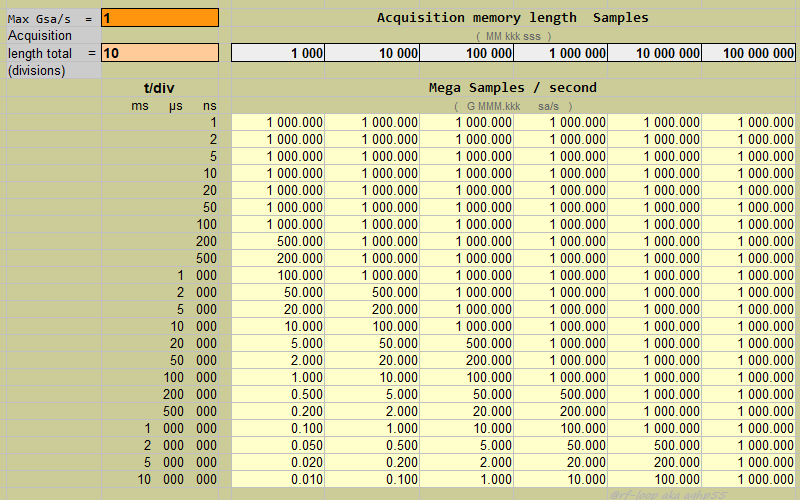
Kuten huomataan, mitä enemmän ottaa asioita huomioon sitä vaikeammaksi ja
mutkikkaammaksi asia käy kuin sen määrittäminen mikä
samplenopeus pitäisi skoopissa olla ja paljonko kaistaleveyttä ym.
Mikäli aletaan puhua esimerkiksi nousu- ja laskuaikojen mittaaamisesta ja
mittauksen tarkkuudesta asia senkun laajenee. Ei ole mitään yhtä vastausta.
Vähintään yhtä hankala on vastata kysymykseen - millaisia ne signaalit ovat
joita minun pitää voida oskilloskoopilla tutkia ja mitata jollain haluamallani
tarkkuudella.
Voisi sanoa kansalliseen tyyliin "Eihän tästä ota kuopion povarikaan selvää". Ja se
toteamus on aika hyvä.
--» Ylös
--» Oskilloskoopit
--» Etusivulle - Home